Temas
- Encuentra la ecuación cuadrática
- Factorización
- Encontrar el valor k
- Encuentra los valores que se te piden
- Ejercicio para calcular edades
- Cálculo de un terreno
- Triángulos proporcionales
- Calcula el área del jardín
- Criterio de semejanza en rectángulos
- Calcula el numero que se te indica
- Estructura la ecuación cuadrática y calcula
- Calcular tiempo de llenado de una piscina
- Encuentra los valores que se indican
- Cálculo de un volumen
- Llenando un deposito
Bienvenidos a nuestra sección dedicada a la resolución de Problemas de Ecuaciones Cuadráticas. Las ecuaciones cuadráticas representan un componente esencial de las matemáticas, y su comprensión y manejo son cruciales para abordar desafíos matemáticos complejos. En esta guía, le proporcionaremos una orientación paso a paso sobre la resolución de ecuaciones cuadráticas.
El proceso de resolver una ecuación cuadrática comienza al igualar una expresión polinómica de segundo órden a cero, seguido de la aplicación de métodos rigurosos como la factorización, la fórmula cuadrática o el método de completar el cuadrado para determinar las soluciones. A medida que avanzamos en este proceso, desvelamos las soluciones matemáticas inherentes a situaciones complejas.
Encuentra la ecuación cuadrática
 
1 Escribir una ecuación de segundo grado cuyas soluciones son: 3 y −2.
1Como conocemos las raíces de la ecuación, podemos escribir ésta como:
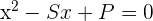
Siendo  la suma de las raíces y
la suma de las raíces y  el producto de las raíces
el producto de las raíces
2Calculamos  y
y 

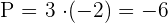
3La ecuación de segundo grado buscada es

2 Escribir una ecuación de segundo grado cuyas soluciones son: 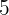 y
y 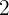
1Ahora, ambas raíces son positivas, por lo que consideramos la ecuación:
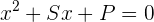
Siendo  la suma de las raíces y
la suma de las raíces y  el producto de las raíces
el producto de las raíces
2Calculamos 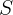 y
y 
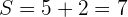
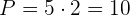
3La ecuación de segundo grado buscada es

 
Factorización
 
3 Factorizar 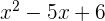
1Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
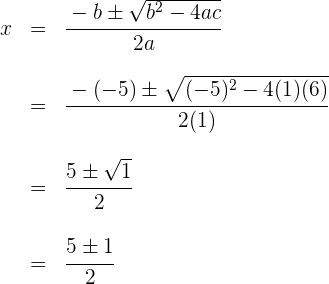
Las raíces son

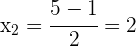
2Conociendo las raíces de la ecuación podemos factorizar de este modo:
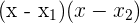
3Así, la factorización buscada es
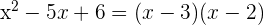
4 Factorizar 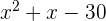
1Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado


2Conociendo las raíces de la ecuación podemos factorizar de este modo:
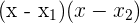
3Así, la factorización buscada es
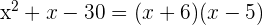
 
Encontrar el valor k
 
5 Determinar  de modo que en la ecuación
de modo que en la ecuación 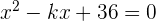 las raíces sean iguales.
las raíces sean iguales.
1Para que las dos raíces sean iguales, el discriminante  tiene que ser igual a cero.Calculamos el discriminante
tiene que ser igual a cero.Calculamos el discriminante

2Igualamos el resultado a cero
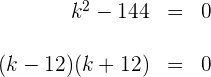
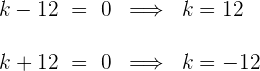
3Igualamos cada factor a cero y buscamos los valores de  que hacen que las raíces sean guales
que hacen que las raíces sean guales
6 Determinar  de modo que en la ecuación
de modo que en la ecuación  las raíces sean iguales.
las raíces sean iguales.
1Para que las dos raíces sean iguales, el discriminante 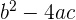 tiene que ser igual a cero. Calculamos el discriminante
tiene que ser igual a cero. Calculamos el discriminante

2Igualamos el resultado a cero

3Igualamos cada factor a cero y buscamos los valores de  que hacen que las raíces sean guales
que hacen que las raíces sean guales

 
Encuentra los valores que se te piden
 
7La suma de dos números es 5 y su producto es −84. Halla dichos números.
1Si conocieramos las raíces de la ecuación, podríamos escribir ésta como:
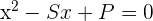
Siendo  la suma de las raíces y
la suma de las raíces y  el producto de las raíces
el producto de las raíces
2Sabemos que 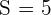 y
y 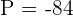 , por lo que obtenemos
, por lo que obtenemos
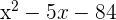
3Resolvemos la ecuación de segundo grado 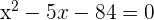
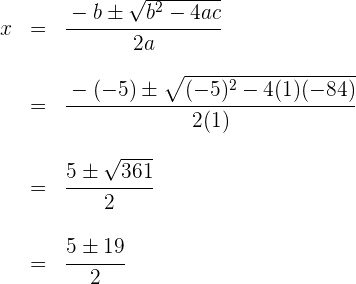
Las raíces son
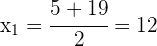
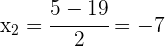
Así, los números buscados son  y
y 
8La suma de dos números es -4 y su producto es -21. Halla dichos números.
1Si conocieramos las raíces de la ecuación, podríamos escribir ésta como:
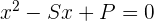
Siendo 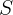 la suma de las raíces y
la suma de las raíces y  el producto de las raíces
el producto de las raíces
2Sabemos que 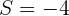 y
y 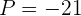 , por lo que obtenemos
, por lo que obtenemos
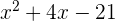
3Resolvemos la ecuación de segundo grado 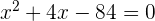

Las raíces son

Así, los números buscados son  y
y 
 
Ejercicio para calcular edades
 
9Dentro de 11 años la edad de Pedro será la mitad del cuadrado de la edad que tenía hace 13 años. Calcula la edad de Pedro.
1Designamos las variables para el ejercicio:
Edad actual 
Edad hace 13 años 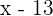
Edad dentro de 11 años 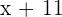
2Escribimos la ecuación correspondiente:
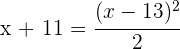
3Elevamos el binomio al cuadrado, quitamos denominadores y obtenemos la ecuación
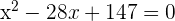
4Resolvemos la ecuación
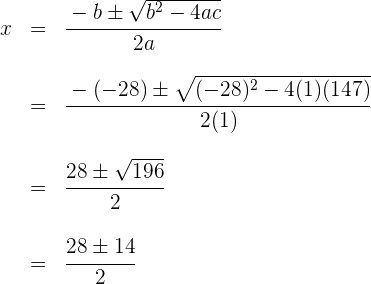
Las raíces son
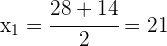

 no es una solución válida porque entonces ¿qué edad tendría hace 13 años?
no es una solución válida porque entonces ¿qué edad tendría hace 13 años?
Así, la edad actual es  años
años
10Dentro de 9 años, la edad de Ana será igual a un cuarto del cuadrado de la edad que tenía hace 15 años. ¿Cuál es la edad actual de Ana?
1Designamos las variables para el ejercicio:
Edad actual 
Edad hace 15 años 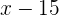
Edad dentro de 9 años 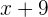
2Escribimos la ecuación correspondiente:
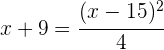
3Elevamos el binomio al cuadrado, quitamos denominadores y obtenemos la ecuación

4Resolvemos la ecuación

Las raíces son

La edad 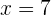 en este contexto no tiene sentido, ya que estamos hablando de una persona que existió al menos 15 años. Entonces, Ana tiene 27 años.
en este contexto no tiene sentido, ya que estamos hablando de una persona que existió al menos 15 años. Entonces, Ana tiene 27 años.
 
Cálculo de un terreno
 
11Para vallar una finca rectangular de  se han utilizado
se han utilizado 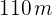 de cerca. Calcula las dimensiones de la finca.
de cerca. Calcula las dimensiones de la finca.
1Representamos el terreno

donde
Semiperímetro 
Base 
Altura 
2El área es igual a base por altura
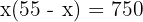
3Quitamos paréntesis y hallamos las raíces
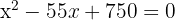
 y
y 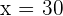
Así, las dimensiones de la finca son:
base  y altura
y altura 
base  y altura
y altura 
12Para vallar una finca rectangular de 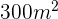 , se han utilizado
, se han utilizado 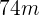 de cerca. Calcula las dimensiones de la finca.
de cerca. Calcula las dimensiones de la finca.
1Representamos el terreno

donde
Semiperímetro 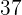
Base 
Altura 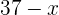
2El área es igual a base por altura
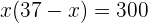
3Desarrollamos el producto y obtenemos la ecuación
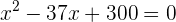
Entonces, usamos la fórmula cuadrática para encontrar las raíces:

Entonces, las raíces son

Así, las dimensiones de la finca son:
base 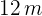 y altura
y altura  , o, de manera equivalente,
, o, de manera equivalente,
base  y altura
y altura 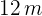
 
Triángulos proporcionales
 
13Los tres lados de un triángulo rectángulo son proporcionales a los números 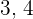 y
y  . Halla la longitud de cada lado sabiendo que el área del triángulo es
. Halla la longitud de cada lado sabiendo que el área del triángulo es 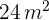 .
.
1Representamos los datos proporcionados

Primer lado  (base)
(base)
Segundo lado  (altura)
(altura)
Tercer lado 
2Aplicamos la fórmula del área de un triángulo

3Quitamos denominadores y resolvemos la ecuación

 no es solución porque un lado no puede tener una longitud negativa. Así las soluciones son:
no es solución porque un lado no puede tener una longitud negativa. Así las soluciones son:
Primer lado 
Segundo lado 
Tercer lado 
14Dos lados de un triángulo isósceles son proporcionales a 10, y el lado restante a 12. Halla la longitud de cada lado sabiendo que el área del triángulo es 
1Representamos los datos proporcionados

Lados iguales: 
Lado distinto:  (base)
(base)
Para obtener una fórmula con respecto a  del área del triángulo, primero debemos encontrar la altura
del área del triángulo, primero debemos encontrar la altura  . Por el Teorema de Pitágoras,
. Por el Teorema de Pitágoras,

Entonces, 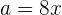
.
2Aplicamos la fórmula del área de un triángulo

3Despejamos para  :
:

Como no podemos tener lados de longitud negativa, la respuesta correcta es 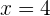 . Es decir, nuestro triángulo tiene base
. Es decir, nuestro triángulo tiene base 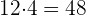 y lados
y lados  .
.
 
Calcula el área del jardín
 
15Un jardín rectangular de  de largo por
de largo por 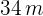 de ancho está rodeado por un camino de arena uniforme. Halla la anchura de dicho camino si se sabe que su área es
de ancho está rodeado por un camino de arena uniforme. Halla la anchura de dicho camino si se sabe que su área es  .
.
1Representamos los datos proporcionados

Llamaremos  a la anchura del camino
a la anchura del camino
2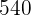 será igual al área total del conjunto menos el área del jardín
será igual al área total del conjunto menos el área del jardín
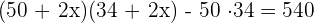
3Quitamos paréntesis, operamos y simplificamos la ecuación dividiendo por 4 en los dos miembros
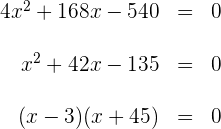
Así, la anchura del camino es  .
.
 no es una solución porque las distancias han de ser positivas.
no es una solución porque las distancias han de ser positivas.
16Una zanja tiene de 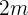 de ancho y
de ancho y 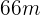 de largo. Si queremos agregar césped alrededor de la zanja, y que tenga un área total de de
de largo. Si queremos agregar césped alrededor de la zanja, y que tenga un área total de de 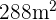 , ¿cuán ancho debe ser este márgen de césped?
, ¿cuán ancho debe ser este márgen de césped?
1Representamos los datos proporcionados
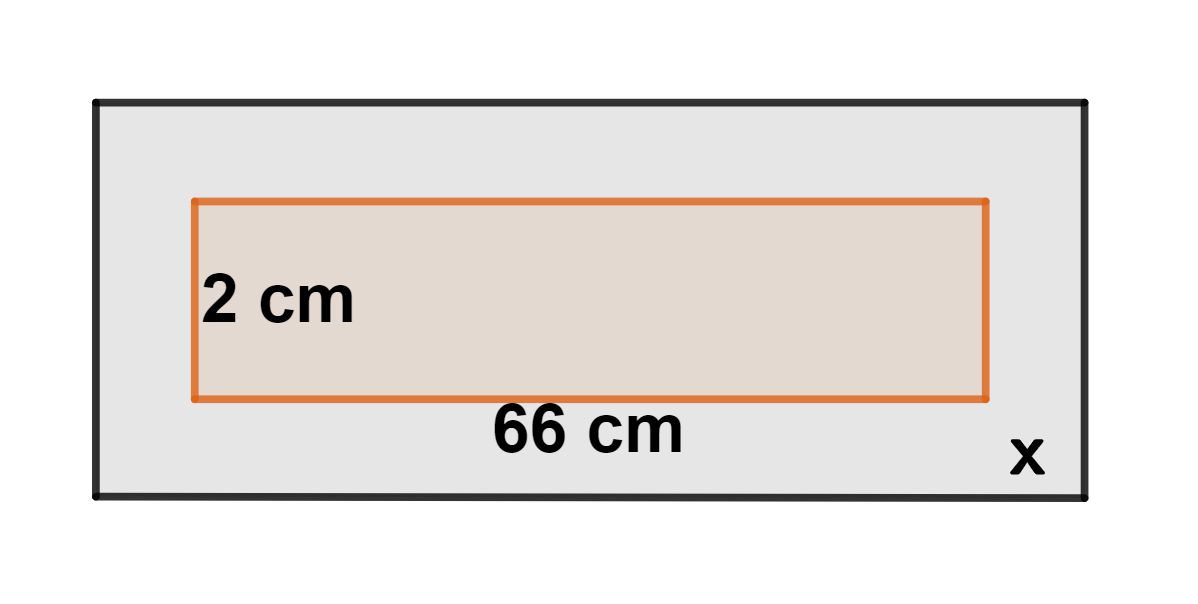
Sea  la anchura del márgen de pasto.
la anchura del márgen de pasto.
2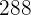 será igual al área total del conjunto sin la zanja:
será igual al área total del conjunto sin la zanja:

3Expandimos el producto de polinomios y simplificamos la expresión:

Las raíces son entonces 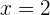 y
y  . Como estamos tratando con distancias (parámetro positivo), solamente la primera solución tiene sentido. Entonces, necesitamos un márgen de
. Como estamos tratando con distancias (parámetro positivo), solamente la primera solución tiene sentido. Entonces, necesitamos un márgen de 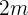 de pasto.
de pasto.
 
Criterio de semejanza en rectángulos
 
17Calcula las dimensiones de un rectángulo cuya diagonal mide 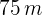 , sabiendo que es semejante a otro rectángulo cuyos lados miden
, sabiendo que es semejante a otro rectángulo cuyos lados miden 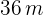 y
y 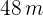 respectivamente.
respectivamente.
1Los lados tienen en común el 12, por lo que empleando la semejanza se tiene
Base 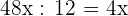
Altura 
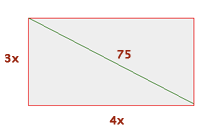
2Aplicamos el teorema de Pitágoras
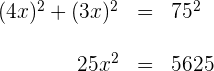
3Resolvemos la última ecuación y obtenemos 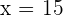 . Así, las dimensiones del rectángulo solicitado son:
. Así, las dimensiones del rectángulo solicitado son:
Base 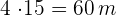
Altura 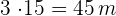
18Calcula las dimensiones de un rectángulo cuya diagonal mide  , sabiendo que es semejante a otro rectángulo cuyos lados miden
, sabiendo que es semejante a otro rectángulo cuyos lados miden 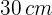 y
y  respectivamente.
respectivamente.
1Los lados tienen en común el 5, por lo que empleando la semejanza se tiene
Base 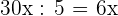
Altura 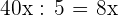
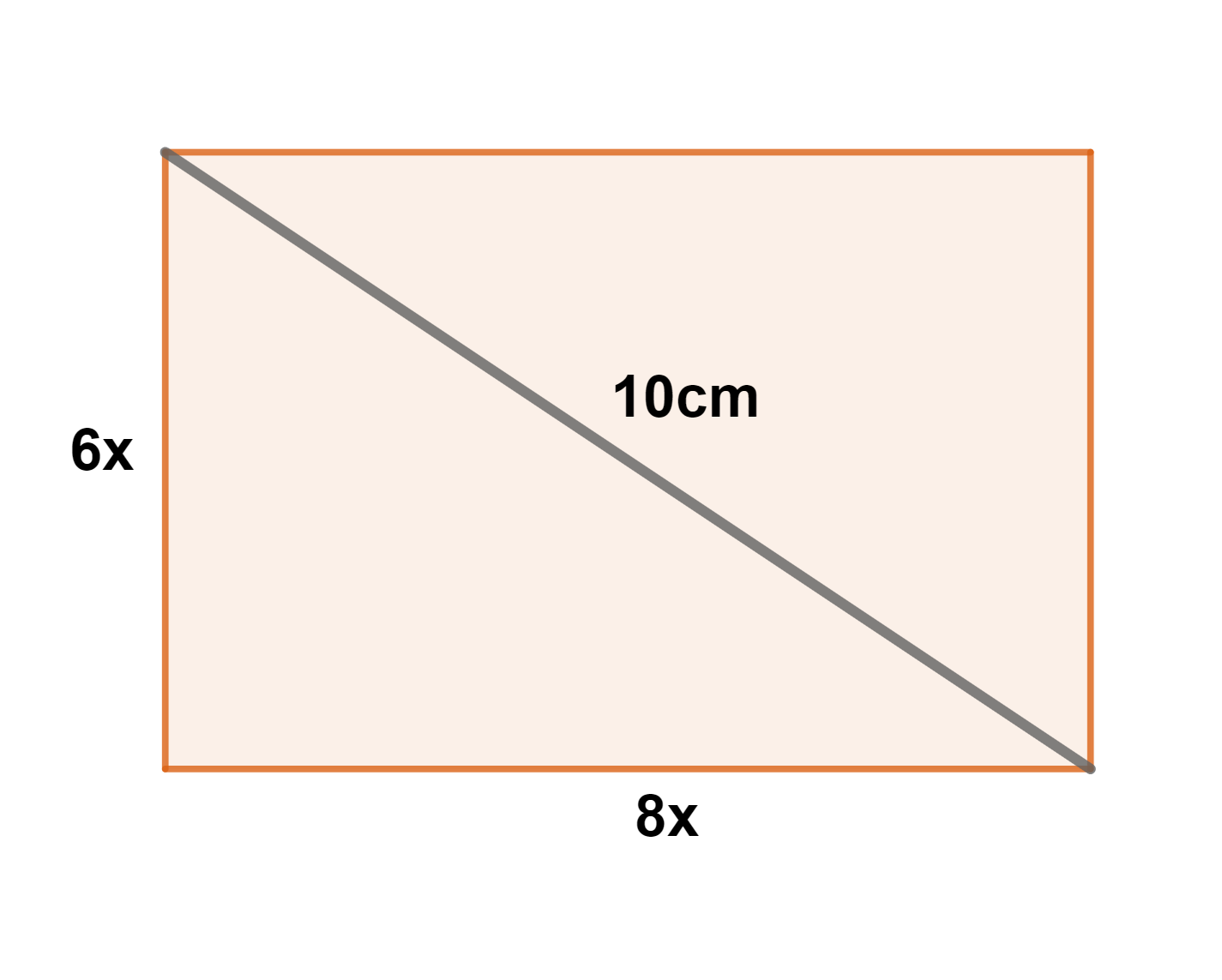
2Aplicamos el teorema de Pitágoras

Es decir, la base mide 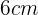 y la altura
y la altura 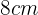
 
Calcula el numero que se te indica
 
19Halla un número entero sabiendo que la suma con su inverso es  .
.
1Consideramos
Número: 
Inverso del número: 
2Realizamos la suma indicada
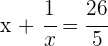
3Resolvemos la ecuación racional
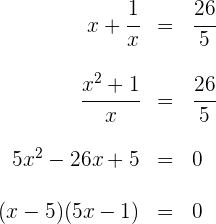
Las soluciones de la ecuación son  y
y 
El número pedido es  , pues
, pues  no es solución porque no es un número entero.
no es solución porque no es un número entero.
20Halla un número entero sabiendo que la suma con su inverso es 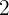 .
.
1Consideramos
Número: 
Inverso del número: 
2Realizamos la suma indicada
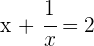
3Resolvemos la ecuación racional

Las soluciones de la ecuación son 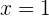 y
y 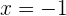 . Sin embargo, sustituir
. Sin embargo, sustituir 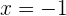 en la expresión inicial no expresa lo que necesitamos. Por lo tanto, la respuesta es
en la expresión inicial no expresa lo que necesitamos. Por lo tanto, la respuesta es 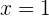 .
.
 
Estructura la ecuación cuadrática y calcula
 
21Dos números naturales se diferencian en dos unidades y la suma de sus cuadrados es 580. ¿Cuáles son esos números?
1Consideramos
Primer número 
Segundo número 
Expresamos la suma de los cuadrados
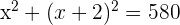
2Elevamos el binomio al cuadrado, operamos y simplificamos la ecuación
dividiendo en los dos miembros por 2
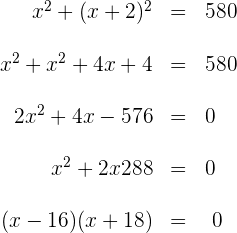
3Las soluciones de la ecuación son  y
y 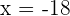
Primer número 
segundo número 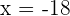
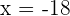 no es solución a nuestro problema porque no es un número natural
no es solución a nuestro problema porque no es un número natural
22Dos números naturales se diferencian en cinco unidades y la suma de sus cuadrados es 277. ¿Cuáles son esos números?
1Sea  el primer número y
el primer número y  el segundo. Expresamos su suma de cuadrados como
el segundo. Expresamos su suma de cuadrados como

2Elevamos el binomio al cuadrado, operamos y simplificamos la ecuación:

3Las soluciones de la ecuación son  y
y 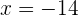 . Como -14 no es un número natural, tomamos
. Como -14 no es un número natural, tomamos  . Entonces, 9 y 14 son los números requeridos.
. Entonces, 9 y 14 son los números requeridos.
 
Calcular tiempo de llenado de una piscina
 
23Dos caños  y
y 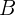 llenan juntos una piscina en dos horas,
llenan juntos una piscina en dos horas,  lo hace por sí solo en tres horas menos que
lo hace por sí solo en tres horas menos que 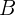 . ¿Cuántas horas tarda cada uno separadamente?
. ¿Cuántas horas tarda cada uno separadamente?
1Consideramos
Tiempo de 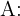

Tiempo de 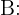

2En una hora ocurre lo siguiente:

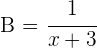
También sabemos que en una hora, los 2 caños juntos llenan media piscina

3Sustituimos:
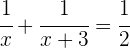
Tenemos una ecuación racional; para resolver primero tenemos que quitar denominadores
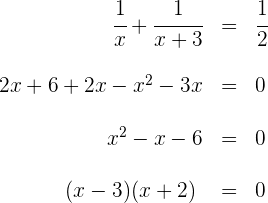
Así, las posibles soluciones son  y
y  , pero esta última no es solución ya que el tiempo sería negativo.
, pero esta última no es solución ya que el tiempo sería negativo.
4Comprobamos que  es una solución:
es una solución:
Al cabo de una hora, ocurre que:

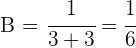
Al cabo de 2 horas:
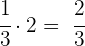

Entonces, en 2 horas la piscina se habrá llenado
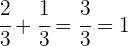
La piscina estará completamente llena al cabo de 2 horas. Así, el tiempo solicitado es:
Tiempo de 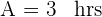
Tiempo de 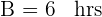
24Dos caños  y
y 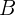 llenan juntos una piscina en seis horas,
llenan juntos una piscina en seis horas,  lo hace por sí solo en cinco horas menos que
lo hace por sí solo en cinco horas menos que 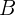 . ¿Cuántas horas tarda cada uno separadamente?
. ¿Cuántas horas tarda cada uno separadamente?
1Sea 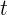 el tiempo (en horas) que tarda
el tiempo (en horas) que tarda  en llenar la piscina. Entonces,
en llenar la piscina. Entonces, 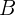 tarda
tarda  en llenar la piscina. En otras palabras, el grifo
en llenar la piscina. En otras palabras, el grifo  vierte
vierte  de la capacidad total de la piscina por hora. Similarmnte, el grifo
de la capacidad total de la piscina por hora. Similarmnte, el grifo 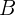 vierte
vierte  de la capacidad total de la piscina por hora. También sabemos que en una hora, los 2 caños juntos llenan un quinto de la piscina:
de la capacidad total de la piscina por hora. También sabemos que en una hora, los 2 caños juntos llenan un quinto de la piscina:
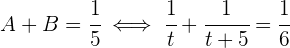
Tenemos una ecuación racional; por lo que la simplificamos para deshacernos de los denominadores:

Así, las posibles soluciones son  y
y 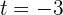 , pero esta última no es solución ya que el tiempo sería negativo.
, pero esta última no es solución ya que el tiempo sería negativo.
4Comprobamos que  es una solución al problema. Es decir, debe ocurrir que en 6 horas, los grifos llenan la piscina:
es una solución al problema. Es decir, debe ocurrir que en 6 horas, los grifos llenan la piscina:

 
Encuentra los valores que se indican
 
25Los lados de un triángulo rectángulo tienen por medidas en centímetros tres
números pares consecutivos. Halla los valores de dichos lados.
1Representamos los datos proporcionados
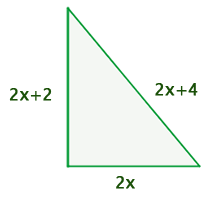
Primer cateto 
Segundo cateto 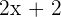
Hipotenusa 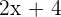
2Aplicamos el teorema de Pitágoras
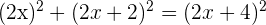
3Elevamos los binomios al cuadrado, operamos y simplificamos la ecuación
dividiendo en los dos miembros por 4
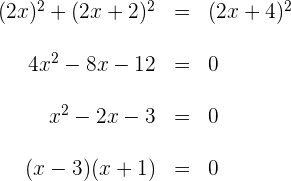
4Las soluciones de la ecuación son 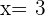 y
y 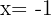 . Así, las medidas solicitadas corresponden a
. Así, las medidas solicitadas corresponden a 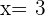
Primer cateto 
Segundo cateto 
Hipotenusa 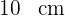
No consideramos  porque las distancias son positivas
porque las distancias son positivas
26Los lados de un triángulo rectángulo tienen por medidas en centímetros de tres números múltiplos de 5, consecutivos (por ejemplo, 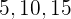 ). Halla los valores de dichos lados.
). Halla los valores de dichos lados.
1Representamos los datos proporcionados
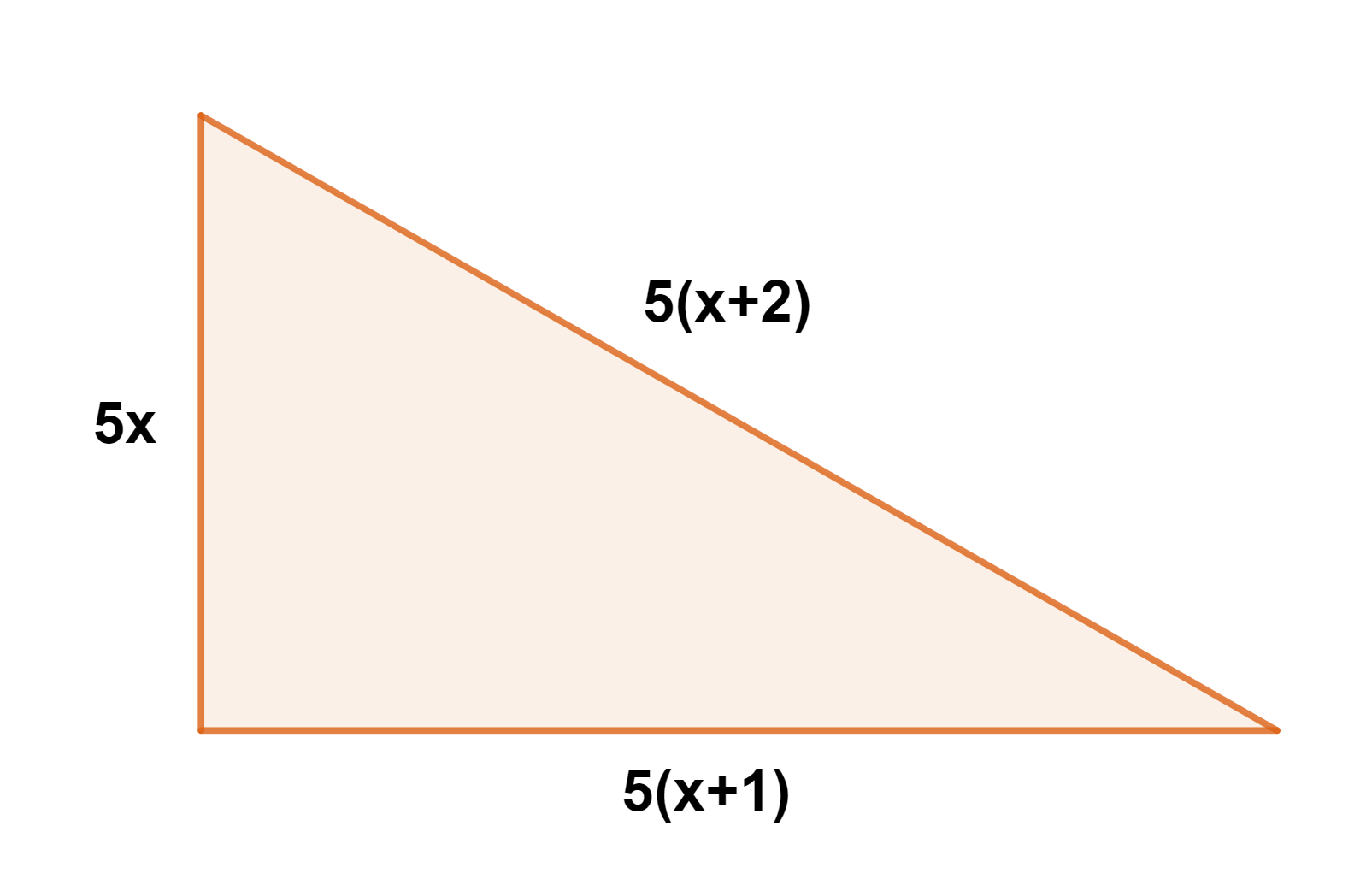
Recordemos que un múltiplo de 5 puede ser escrito como  , donde
, donde  representa un número entero. Entonces, nuestro triángulo tiene las siguientes medidas:
representa un número entero. Entonces, nuestro triángulo tiene las siguientes medidas:
Primer cateto 
Segundo cateto 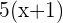
Hipotenusa 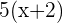
2Aplicamos el Teorema de Pitágoras:

3Elevamos los binomios al cuadrado, operamos y simplificamos la ecuación
dividiendo todo por 25

4Las soluciones de la ecuación son 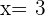 y
y 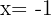 . Así, las medidas solicitadas corresponden a
. Así, las medidas solicitadas corresponden a 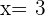
Primer cateto 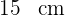
Segundo cateto 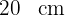
Hipotenusa 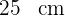
No consideramos  porque las distancias son positivas
porque las distancias son positivas
 
Cálculo de un volumen
 
27Una pieza rectangular es 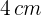 más larga que ancha. Con ella se construye una caja de
más larga que ancha. Con ella se construye una caja de 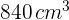 cortando un cuadrado de
cortando un cuadrado de 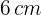 de lado en cada esquina y doblando los bordes. Halla las dimensiones de la caja.
de lado en cada esquina y doblando los bordes. Halla las dimensiones de la caja.
1Representamos los datos proporcionados
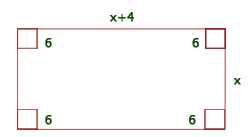
Ancho: 
Largo: 
Alto: 
2El volumen de la caja, que es prisma rectangular, es: 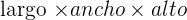
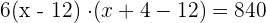 (x − 12) · (x −8) = 140
(x − 12) · (x −8) = 140
3Resolvemos la ecuación anterior

Las soluciones de la ecuación son  y
y  . Así, las medidas solicitadas son
. Así, las medidas solicitadas son
Ancho: 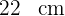
Largo: 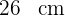
La solución  la rechazamos porque una longitud no puede ser negativa
la rechazamos porque una longitud no puede ser negativa
28Una pieza rectangular es 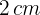 más corta que ancha. Con ella se construye una caja de
más corta que ancha. Con ella se construye una caja de 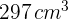 cortando un cuadrado de
cortando un cuadrado de 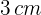 de lado en cada esquina y doblando los bordes. Halla las dimensiones de la caja.
de lado en cada esquina y doblando los bordes. Halla las dimensiones de la caja.
1Representamos los datos proporcionados
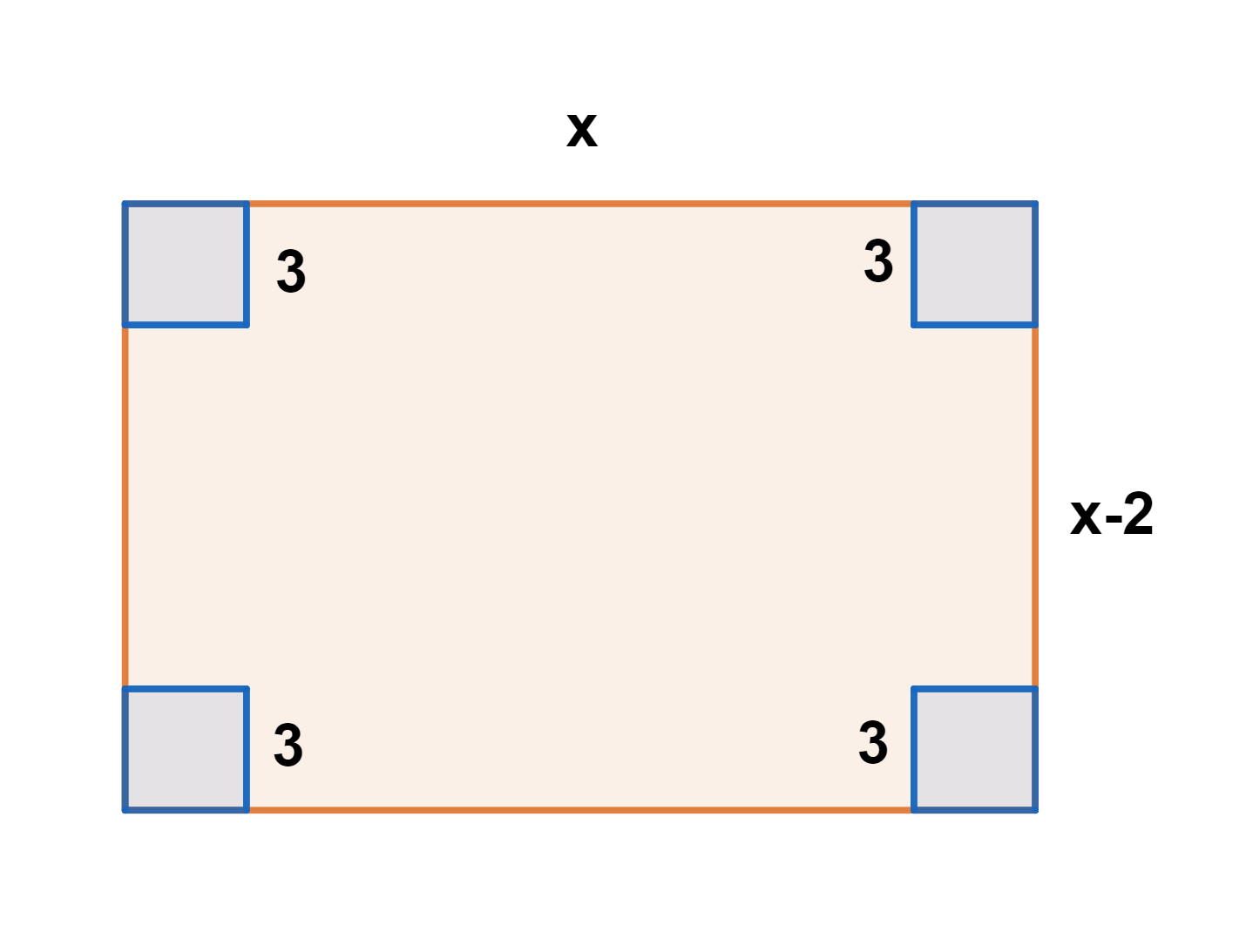
Ancho: 
Largo: 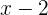
Alto: 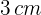
2El volumen de la caja, que es prisma rectangular, es: 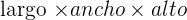
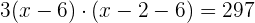
3Resolvemos la ecuación anterior

Las soluciones de la ecuación son  y
y 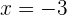 . Así, las medidas solicitadas son
. Así, las medidas solicitadas son
Ancho: 
Largo: 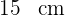
La solución  la rechazamos porque una longitud no puede ser negativa
la rechazamos porque una longitud no puede ser negativa
 
Llenando un deposito
 
29Un caño tarda dos horas más que otro en llenar un depósito y abriendo los dos juntos se llena en 1 hora y 20 minutos. ¿Cuánto tiempo tardará en llenarlo cada uno por separado?
1Consideramos
Tiempo del primero: 
Tiempo del segundo: 
2En una hora ocurre lo siguiente:
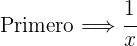
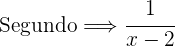
También sabemos que en una hora y 20 minutos, esto es en  de hora los 2 caños juntos llenan un depósito
de hora los 2 caños juntos llenan un depósito
3Sustituimos:
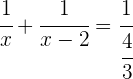
Tenemos una ecuación racional; para resolver primero tenemos que quitar denominadores
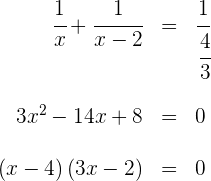
Así, las posibles soluciones son  y
y  , pero esta última no es solución ya que el tiempo empleado por el segundo caño sería negativo.
, pero esta última no es solución ya que el tiempo empleado por el segundo caño sería negativo.
4Así, los tiempos empleados son:
Tiempo del primero 
Tiempo del segundo 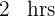
30Un caño tarda cinco horas más que otro en llenar un depósito y abriendo los dos juntos se llena en 3 horas y 20 minutos. ¿Cuánto tiempo tardará en llenarlo cada uno por separado?
1Sea 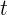 el tiempo que tarda el primer caño en llenar el depósito. Entonces, el segundo tarda
el tiempo que tarda el primer caño en llenar el depósito. Entonces, el segundo tarda 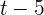 . En una hora, el primer caño llena
. En una hora, el primer caño llena  de la cantidad máxima del depósito, mientras que el segundo llena
de la cantidad máxima del depósito, mientras que el segundo llena  .
.
También sabemos que en tres hora y 20 minutos, ese decir,  de hora, los 2 caños juntos llenan el depósito por completo.
de hora, los 2 caños juntos llenan el depósito por completo.
3Sustituimos:
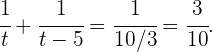
Tenemos una ecuación racional; para resolver, primero tenemos que quitar denominadores

Así, las posibles soluciones son  y
y  , pero esta última no es solución ya que el tiempo empleado por el segundo caño sería negativo.
, pero esta última no es solución ya que el tiempo empleado por el segundo caño sería negativo.
4Así, los tiempos empleados son:
Tiempo del primero 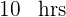
Tiempo del segundo 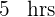
-



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
x²-6x+8=0
x²+6x=0-8
4x=-8
x=-8/4
x=-2
Hola Valeria, lamento la intromisión, si aún necesitas la respuesta, la ecuación es de segundo grado porque la letra x² es la de mayor exponente, debido a que no tienes término semejantes, como x+x, o x²+x² (por ejemplo) no puedes operarios de manera directa. Puedes utilizar la fórmula de segundo general de segundo grado (Que la puedes encontrar en esta página web y te explica cómo usarla, es muy sencillo) o puedes hacer una factorización, tus resultados son x=4 y x=2.
resolver la ecuacion x−4
3
− 5 = 0
X=4 yx= 2
2X=4+2
X=6/2
X=3