Temas

Ejercicios de sistemas de ecuaciones no lineales
1
Tenemos el siguiente sistema no lineal:

Resolveremos el sistema por sustitución. Primero, despejamos una incógnita de alguna de las ecuaciones, preferentemente de la de primer grado.

Después, sustituimos el valor de la incógnita despejada en la otra ecuación:
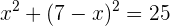
Ahora, resolvemos la ecuación resultante:

Luego, al dividir por 2, obtenemos la siguiente ecuación cuadrática,
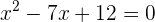
La solución de esta ecuación se obtiene mediante la fórmula general,

Por lo que las soluciones a la ecuación cuadrática son:

Cada uno de los valores obtenidos se sustituyen en la otra ecuación. De este modo, se obtienen los valores correspondientes de la otra incógnita.

Por tanto, las soluciones al sistema son

2
Nuestro sistema de ecuaciones ahora es

De nuevo, vamos a resolver el sistema por sustitución. Primero, despejamos la  de la primera ecuación:
de la primera ecuación:
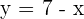
Después, sustituimos el valor de  en la segunda ecuación:
en la segunda ecuación:

Es decir,
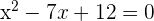
Ahora, resolvemos la ecuación resultante utilizando la fórmula general
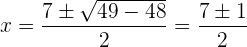
Así, las soluciones de la ecuación cuadrática son:

Por último, sustituimos en la otra ecuación cada uno de los valores que acabamos de obtener. Así, obtendremos los valores correspondientes de la otra incógnita:


3
En este caso, nuestro sistema está dado por:

De nuevo, el sistema lo resolveremos utilizando sustitución. Primero, despejamos la  de la segunda ecuación:
de la segunda ecuación:

Sustituimos el valor de  en la primera ecuación
en la primera ecuación

Agrupamos términos semejantes y, después, dividimos por 2:
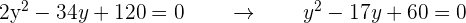
Resolvemos la ecuación resultante,
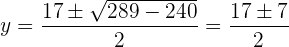
Por lo que la ecuación cuadrática tiene soluciones
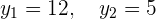
Sustituimos en la otra ecuación cada uno de los valores obtenidos. De esta manera, obtenemos los valores de la otra incógnita,

Por tanto, las soluciones son:

4
Tenemos ahora el sistema,

Resolvemos el sistema, de nuevo, por sustitución. Ya tenemos despejada la  en la primera ecuación, de manera que sustituimos el valor de
en la primera ecuación, de manera que sustituimos el valor de  en la segunda ecuación.
en la segunda ecuación.

Como es una ecuación radical elevamos al cuadrado en ambos lados de la ecuación (observa que primero dejamos la raíz sola del lado izquierdo de la ecuación):

Luego,
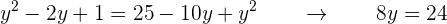
Por lo que . Comprobamos la solución de la ecuación radical

Es decir, , por lo que
sí es solución de la ecuación radical. Sustituimos, en la otra ecuación, el valor obtenido. Así, obtenemos el valor de la otra incógnita:
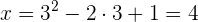

5
Nuestro sistema ahora está dado por:

Para resolver el sistema en primer lugar vamos a realizar dos cambios de variable:
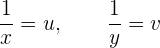
Sustituimos los cambios de variable en el sistema,

Ya tenemos un sistema que es más fácil de resolver. De nuevo resolveremos este sistema por sustitución. Despejamos  de la segunda ecuación, lo que nos da
de la segunda ecuación, lo que nos da  . Si sustituimos en la primera ecuación, tenemos
. Si sustituimos en la primera ecuación, tenemos
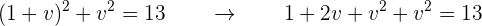
Que, al igualar a cero y dividir por 2, obtenemos,

Resolvemos la ecuación resultante por medio de la fórmula general,
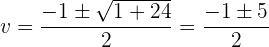
Por lo que tenemos
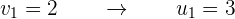
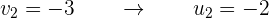
Deshacemos el cambio y cada uno de los valores obtenidos se sustituyen en la otra ecuación, se obtienen así los valores correspondientes de la otra incógnita
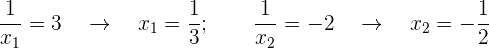
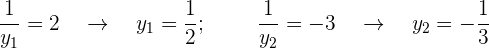
Así, las soluciones son:

Problemas que utilizan sistemas de ecuaciones no lineales
6 El producto de dos números es 4, y la suma de sus cuadrados 17. ¿Cuáles son esos números?
El producto de dos números es 4, y la suma de sus cuadrados 17. ¿Cuáles son esos números?
Para resolver este problema, primero debemos expresarlo de manera algebraica. Observemos primero que "el producto de dos números es 4" se puede expresar algebraicamente como . Similarmente, "la suma de sus cuadrados (de estos dos números) es 17" se expresa algebraicamente como
. Por lo tanto, obtenemos el siguiente sistema no lineal de ecuaciones:

Resolveremos por sustitución. Primero, despejamos  de la primera ecuación,
de la primera ecuación,
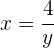
Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
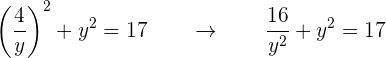
Es decir,
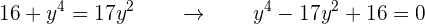
Por lo que obtenemos una ecuación bicuadrada, la cual debemos resolver. Para resolverla, utilizamos el cambio de variable . Al sustituir este cambio de variable obtenemos,

El cual resolvemos utilizando la fórmula general,
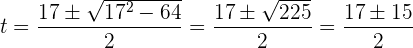
De modo que las soluciones de la ecuación bicuadrada son
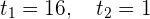
Esto implica que

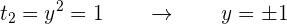
Es decir, tenemos 4 posibles valores para . Por lo tanto, al sustituir estos valores en la primera ecuación, tenemos,

Así, las 4 soluciones del problema son:

7 Halla una fracción equivalente a cuyos términos elevados al cuadrado sumen 1184
Para expresar algebraicamente este problema, la fracción equivalente tendrá como numerador  y como denominador
y como denominador  . De este modo, el problema se resuelve utilizando el siguiente sistema no lineal:
. De este modo, el problema se resuelve utilizando el siguiente sistema no lineal:

Resolvemos el sistema por sustitución. Despejamos primero la  de la primera ecuación:
de la primera ecuación:

Sustituimos el valor de  en la segunda ecuación
en la segunda ecuación
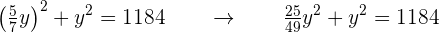
Así

Es decir,
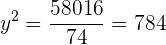
Resolvemos esta ecuación de segundo grado,
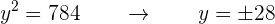
Luego, sustituimos en la otra ecuación cada uno de los valores obtenidos:

Por lo tanto, las fracciones equivalentes a son
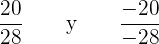













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
x²-6x+8=0
x²+6x=0-8
4x=-8
x=-8/4
x=-2
Hola Valeria, lamento la intromisión, si aún necesitas la respuesta, la ecuación es de segundo grado porque la letra x² es la de mayor exponente, debido a que no tienes término semejantes, como x+x, o x²+x² (por ejemplo) no puedes operarios de manera directa. Puedes utilizar la fórmula de segundo general de segundo grado (Que la puedes encontrar en esta página web y te explica cómo usarla, es muy sencillo) o puedes hacer una factorización, tus resultados son x=4 y x=2.
resolver la ecuacion x−4
3
− 5 = 0
X=4 yx= 2
2X=4+2
X=6/2
X=3