Elige la opción correcta:
1Para resolver la ecuación  la aplicación correcta de la fórmula es:
la aplicación correcta de la fórmula es:
Nuestra ecuación es

Identificamos el coeficiente que acompaña al  , el que acompaña a la
, el que acompaña a la  y el término independiente.
y el término independiente.
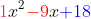
Entonces
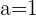
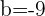
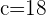
Finalmente sustituimos adecuadamente en la fórmula
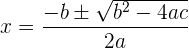
Y obtenemos
2 Las soluciones de la ecuación  son:
son:
Sustituyendo adecuadamente en la fórmula general, tenemos:



Por lo tanto las soluciones son:
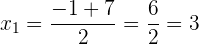

3Para resolver la ecuación 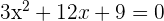 la aplicación correcta de la fórmula es:
la aplicación correcta de la fórmula es:

La primera respuesta es correcta y basta aplicar correctamente la fórmula que hemos visto.
La segunda respuesta también es correcta porque se ha simplificado la ecuación dividiendo entre  , obteniendo así una ecuación equivalente a la original.
, obteniendo así una ecuación equivalente a la original.
Por tanto, ambas respuestas darán lugar a las mismas soluciones.
Tenemos nuestra ecuación original
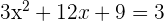
Dividimos todo entre 
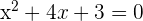
Aplicamos la fórmula general

4Las soluciones de la ecuación 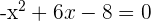 son:
son:
 y
y 
 y
y 
 y
y 
Sustituyendo adecuadamente en la fórmula general, tenemos:
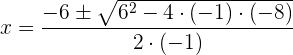
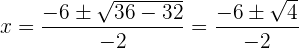
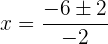
Por lo tanto las soluciones son:
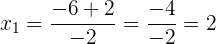

Aunque esta vez hemos resuelto la ecuación aplicando la fórmula sin más, debemos recordar que, generalmente, cuando el coeficiente que acompaña a  es negativo, multiplicamos la ecuación por
es negativo, multiplicamos la ecuación por  :
:
Tenemos nuestra ecuación original
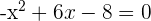
La multiplicamos por 
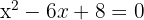
Aplicamos la fórmula general

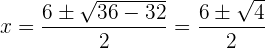
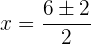
Por lo tanto las soluciones son:
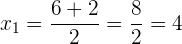
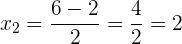
Notamos que coinciden con las obtenidas anteriormente
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
2x+y-z=-1
X-2y+z=5
3x-y-2z=0
Ecuaciones metodo Guss jordan
no entiendo deberían explicar un poco mas detallado
Hola, entendemos tu punto, pero para lograrlo podrías mencionar mas específicamente donde no entendiste y con gusto te ayudamos.
Un cliente en un supermercado ha pagado un total de $312,000 por 24 L de leche 6 kg de jamón y 12 l de aceite de girasol. calcular el precio de cada artículo ,sabiendo que 6 l de aceite cuesta el doble que un jamón más 7 L de leche y que 5 kg de jamón cuesta igual que 10 l de aceite más 4 L de leche resolver esto plis es que lo es que lo he intentado resolver por todos los métodos que me han enseñado de solución como el método de cramer que tiene otro nombre pero no me lo sé como el de reducción método de eliminación método de igualación y el método gráfico
Simplemente traspasas todo al miembro correspondiente y operas, despues traspasas el primer miembro dividiendo al segundo, lo divides y a esta
hola si la ecuación es x+1=10x+10, la respuesta es x=-1, pues si sustituyes el valor queda -1+1=10(-1)+10 o 0=-10+10, que si cumple.