¡Bienvenidos a nuestra página dedicada a problemas y ejercicios resueltos sobre ecuaciones de segundo grado! En esta ocasión, exploraremos el fascinante mundo de las ecuaciones cuadráticas y te proporcionaremos las herramientas necesarias para comprender y resolver estos fundamentales problemas matemáticos.
Las ecuaciones de segundo grado son una parte fundamental de las matemáticas y tienen una amplia aplicación en diversos campos, como la física, la economía y la ingeniería. Estas ecuaciones se caracterizan por tener una incógnita elevada al cuadrado y pueden tener una o dos soluciones reales.
Aquí, exploraremos una amplia variedad de problemas, desde problemas de factorización hasta problemas de aplicación de la fórmula general, y te proporcionaremos explicaciones claras y detalladas para cada paso del proceso de resolución. También, utilizaremos estas técnicas para resolver situaciones del mundo real.
Nuestro objetivo es ayudarte a desarrollar tu comprensión de las ecuaciones de segundo grado, fortalecer tus habilidades de resolución de problemas y fomentar tu confianza en las matemáticas. ¡Así que prepárate para sumergirte en el emocionante mundo de las ecuaciones cuadráticas y descubrir todo lo que pueden ofrecerte!
1Resuelve las siguientes ecuaciones:

1 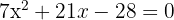
Puede resolverse utilizando la fórmula general o el método de factorización. Aplicando el método de factorización:
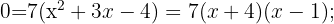

2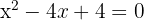
Aplicando el método de factorización:
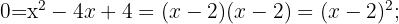
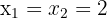
3
Aplicando el método de factorización:


4
Aplicando el método de factorización:


2Resuelve las siguientes ecuaciones:
¿Necesitas un profesor de mates?
1 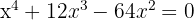
Aplicando el método de factorización:

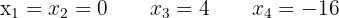
2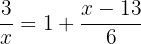
Se escribe el segundo miembro con un común denominador y se hace un producto alternado entre cada miembro por los denominadores. Después, se aplica el método de factorización:



3Resuelve las siguientes ecuaciones:

1
Aplicando el método de factorización, por ejemplo:
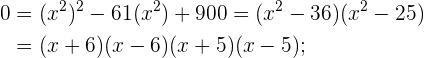

2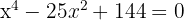
Aplicando el método de factorización:
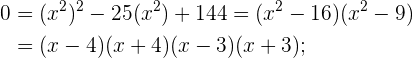

4Resuelve las siguientes ecuaciones:
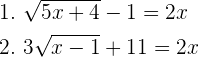
1
Primero se despeja la raíz de la ecuación. Después, se elevan al cuadrado ambos miembros de la igualdad, se desarrollan las potencias y se resuelve.

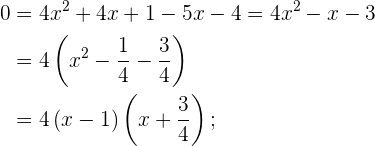

2 
Se despeja la raíz de la ecuación. Después, se elevan al cuadrado ambos miembros de la igualdad, se desarrollan las potencias y se resuelve por la fórmula general.

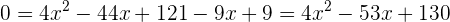

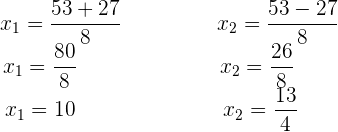
5Hallar las raíces de:
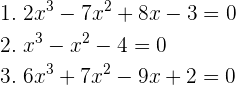
1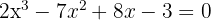
Se emplea la división sintética pues la ecuación es de tercer grado. Los divisores de  son
son 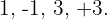 Así:
Así:
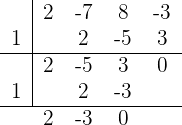
Entonces, la factorización es 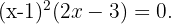 Por tanto:
Por tanto:
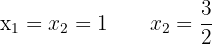
2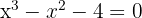
Se emplea la división sintética pues la ecuación es de tercer grado. Los divisores de  son
son 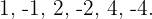 Así:
Así:
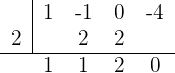
Entonces, la factorización es 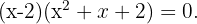 Al calcular el discriminante del trinomio, se concluye que no tiene raíces pues es negativo el resultado. Entonces sólo tiene una solución.
Al calcular el discriminante del trinomio, se concluye que no tiene raíces pues es negativo el resultado. Entonces sólo tiene una solución.
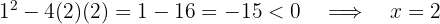
3
Se emplea la división sintética pues la ecuación es de tercer grado. Los divisores de  son
son  Así:
Así:

Entonces, la factorización es  Se resuelve la ecuación cuadrática por la fórmula general:
Se resuelve la ecuación cuadrática por la fórmula general:
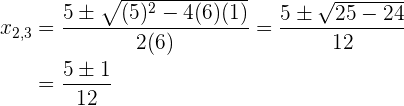
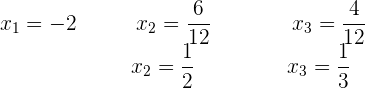
6Resolver los siguientes sistemas de ecuaciones:

1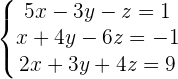
Se construye la matriz de coeficientes asociada al sistema y se reducen las columnas y renglones.
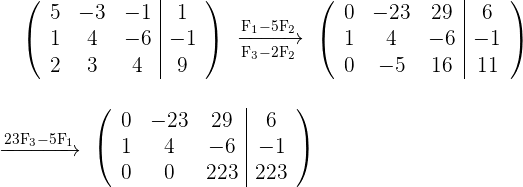
Entonces, 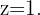 Traduciendo la matriz última al sistema de ecuaciones asociado, se tiene que
Traduciendo la matriz última al sistema de ecuaciones asociado, se tiene que  pues:
pues:
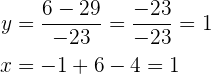
2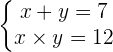
Se despeja una incógnita en la primera ecuación y se sustituye la expresión resultante en la segunda. Después, se resuelve la ecuación cuadrática.
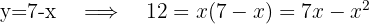
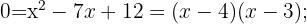

3
Se despeja una incógnita en la primera ecuación y se sustituye la expresión resultante en la segunda. Después, se resuelve la ecuación cuadrática.
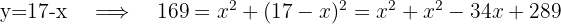


4
Se sustituye la expresión que representa a  en la segunda ecuación. Después se elevan al cuadrado ambos miembros de la ecuación y se resuelve.
en la segunda ecuación. Después se elevan al cuadrado ambos miembros de la ecuación y se resuelve.
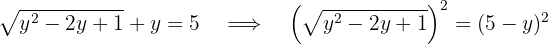


7Determinar el valor de  para que las soluciones de la ecuación
para que las soluciones de la ecuación  sean el mismo valor.
sean el mismo valor.
Se calcula el discriminante y se iguala a cero. Así, se obtiene una raíz doble.
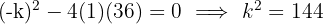
Los valores posibles del coeficiente del término lineal son 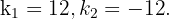
8Hallar el valor de dos números cuya suma sea cinco y su producto 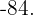

Las parejas de números son  y
y  .
.
9Determinar la edad de Pedro sabiendo que dentro de  años tendra la mitad del cuadrado de la edad que tenía hace
años tendra la mitad del cuadrado de la edad que tenía hace  años.
años.
 la edad que tiene actualmente, hace
la edad que tiene actualmente, hace  años tenía
años tenía 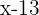 y dentro de
y dentro de  años tendrá
años tendrá  :
: 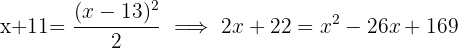

Por tanto, Pedro tiene  años.
años.
10Para cercar una finca rectangular de  se han utilizado
se han utilizado 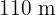 de malla ciclónica. Calcular las dimensiones de la finca.
de malla ciclónica. Calcular las dimensiones de la finca.
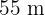 . Por tanto, el problema puede modelarse con las expresiones de la imagen:
. Por tanto, el problema puede modelarse con las expresiones de la imagen: 

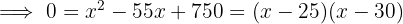
La finca tiene dimensiones de 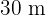 y
y 
11Los tres lados de un triángulo rectángulo son proporcionales a los números  Calcular la longitud de cada lado del tríángulo sabiendo que tiene un área de
Calcular la longitud de cada lado del tríángulo sabiendo que tiene un área de 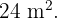
 los lados del triángulo rectángulo de la imagen. A partir de la fórmula para calcular el área puede conocerse dicho factor.
los lados del triángulo rectángulo de la imagen. A partir de la fórmula para calcular el área puede conocerse dicho factor. 
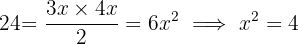
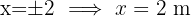
Los lados del triángulo son 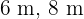 y
y 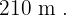
12Un jardín rectangular de 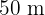 de largo por
de largo por  de ancho está rodeado por un camino de arena de ancho uniforme. Calcular la anchura de dicho camino si se sabe que tiene un área de
de ancho está rodeado por un camino de arena de ancho uniforme. Calcular la anchura de dicho camino si se sabe que tiene un área de 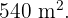
 del camino de arena, se tiene un rectángulo más grande de dimensiones
del camino de arena, se tiene un rectángulo más grande de dimensiones 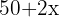 por
por  , como lo indica la figura. Ahora, se expresa el área del camino de arena.
, como lo indica la figura. Ahora, se expresa el área del camino de arena. 

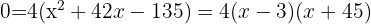
Por tanto, el camino tiene 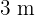 de largo.
de largo.
13Calcular las dimensiones de un rectángulo cuya diagonal mide 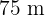 sabiendo que es semejante a otro rectángulo de
sabiendo que es semejante a otro rectángulo de 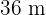 por
por 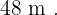
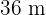 por
por 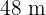 es semejante al rectángulo de
es semejante al rectángulo de 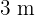 por
por  también lo será el rectángulo cuya diagonal mide
también lo será el rectángulo cuya diagonal mide 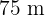 . Se asume, entonces, que sus lados son proporcionales por un factor
. Se asume, entonces, que sus lados son proporcionales por un factor  , como lo muestra la imagen. Se aplica el teorema de Pitágoras y se halla el valor de la incógnita.
, como lo muestra la imagen. Se aplica el teorema de Pitágoras y se halla el valor de la incógnita. 
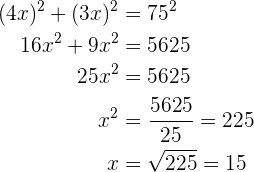
Por tanto, el rectángulo tiene 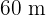 de largo por
de largo por 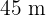 de ancho.
de ancho.
14Hallar un número entero sabiendo que la suma con su inverso es 


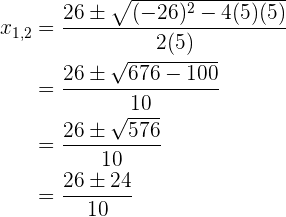
El número es cinco pues la segunda raíz da como resultado una fracción.
15Calcular dos números naturales cuya diferencia es dos y la suma de sus cuadrados es 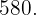
 denota un número, el segundo será
denota un número, el segundo será 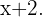
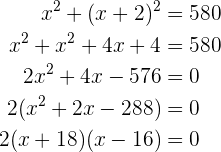
Los números son  y
y 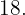
16Dos mangueras A y B llenan juntas una piscina en dos horas. A lo hace por sí sola en tres horas menos que B. Calcular cuántas horas tarda a cada una en llenar la piscina.
 horas en llenar la piscina, la manguera B tardará
horas en llenar la piscina, la manguera B tardará  horas en llenarla. Entonces, cada hora, A llevará llenada
horas en llenarla. Entonces, cada hora, A llevará llenada  partes de la piscina llenada y B,
partes de la piscina llenada y B, 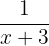 partes. Como al usar ambas mangueras se llena la piscina por completo, se tiene que:
partes. Como al usar ambas mangueras se llena la piscina por completo, se tiene que: 
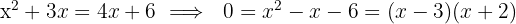
La manguera A tarda  horas en llenar la piscina y la manguera B,
horas en llenar la piscina y la manguera B,  horas.
horas.
17Hallar dos números tales que su producto es cuatro y la suma de sus cuadrados es diecisiete.
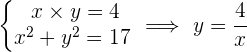

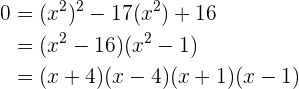
Las parejas de números posibles son 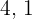 y
y 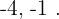
18Hallar una fracción equivalente a  cuyos términos elevados al cuadrado sumen
cuyos términos elevados al cuadrado sumen 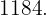
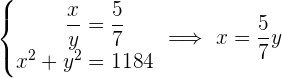
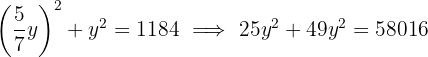

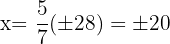
Las fracción que satisface lo solicitado es  , pues en
, pues en 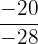 se cancelan los signos negativos y se obtiene la primera fracción.
se cancelan los signos negativos y se obtiene la primera fracción.
19El cliente de un supermercado ha pagado un total de 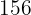 por
por  L de leche,
L de leche,  kg de jamón serrano y
kg de jamón serrano y  L de aceite de oliva. Calcular el precio de cada artículo, sabiendo que un litro de aceite cuesta el triple que un litro de leche y que un kilogramo de jamón cuesta lo mismo que comprar
L de aceite de oliva. Calcular el precio de cada artículo, sabiendo que un litro de aceite cuesta el triple que un litro de leche y que un kilogramo de jamón cuesta lo mismo que comprar  L de aceite más
L de aceite más  L de leche.
L de leche.
 los costos de la leche, el jamón serrano y el aceite de oliva, respectivamente. Se forma el sistema de ecuaciones relacionado y se resuelve.
los costos de la leche, el jamón serrano y el aceite de oliva, respectivamente. Se forma el sistema de ecuaciones relacionado y se resuelve. 
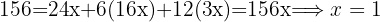

La leche tiene un costo de 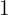 el litro, el jamón serrano de
el litro, el jamón serrano de  el kilogramo y el aceite de oliva,
el kilogramo y el aceite de oliva,  el litro.
el litro.
20Un videoclub está especializado en películas de tres tipos: infantiles, oeste americano y terror. Se sabe que:
El  de las películas infantiles más el
de las películas infantiles más el 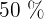 de las del oeste representan el
de las del oeste representan el  del total de las películas.
del total de las películas.
El 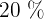 de las películas infantiles más el
de las películas infantiles más el  de las del oeste más del
de las del oeste más del  de las de terror al representan la mitad del total de las películas.
de las de terror al representan la mitad del total de las películas.
Hallar el número de películas de cada tipo sabiendo que hay  películas más del oeste que infantiles.
películas más del oeste que infantiles.
 las películas infantiles, las del oeste y las de terror, respectivamente. Se forma el sistema de ecuaciones relacionado y se resuelte.
las películas infantiles, las del oeste y las de terror, respectivamente. Se forma el sistema de ecuaciones relacionado y se resuelte. 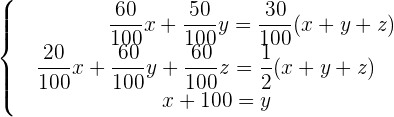
Simplificando el sistema de ecuaciones, se tiene
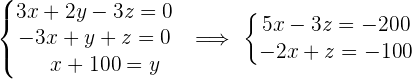
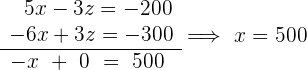
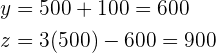
El videoclub tiene  películas infantiles,
películas infantiles,  del oeste y
del oeste y 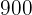 de terror.
de terror.



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
x²-6x+8=0
x²+6x=0-8
4x=-8
x=-8/4
x=-2
Hola Valeria, lamento la intromisión, si aún necesitas la respuesta, la ecuación es de segundo grado porque la letra x² es la de mayor exponente, debido a que no tienes término semejantes, como x+x, o x²+x² (por ejemplo) no puedes operarios de manera directa. Puedes utilizar la fórmula de segundo general de segundo grado (Que la puedes encontrar en esta página web y te explica cómo usarla, es muy sencillo) o puedes hacer una factorización, tus resultados son x=4 y x=2.
2(x-8)+3=x-3
Me parece que el ultimo ejercicio (la tricuadrada) se puede hacer de otra forma ya que hace x^3=t cuando en realidad si se hace x^6=t^3 y x^3=t te da t^3-7t+6 lo cual haciendo un sencillo ruffini te da las x como resultado t=-3 t=2 y t=1 y al volver a pasarlo a las x te da como resultado x1= ∄ y x2= ∄ (al ser la raiz cuadrada de -3) , x3=raiz cuadrada +2, x4= raiz cuadrada -2, x5=+1 y x6=-1. Saludos.
Si haces x^6=t^3 te da x^2=t o x^3=t^(3/2) lo cual complica en vez de facilitar la ecuación, además de que la expresión x^3=t esta mal.
X=4 yx= 2
2X=4+2
X=6/2
X=3