
Repaso sobre la fórmula general
Para resolver ejercicios propuestos, se utilizara la fórmula general para ecuaciones de segundo grado:

La cual se utiliza para resolver toda ecuación de segundo grado del tipo
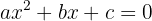 donde
donde 
Utilizar este método es muy sencillo, dado que solo debemos igualar las ecuaciones a cero y sustituir los valores de a,b,c en la fórmula general.
Al resolver una ecuación de segundo grado, pueden ocurrir 3 cosas:
- Existen 2 valores para la variable x que satisfacen la ecuación.
- Existe una única solución.
- La solución no pertenece al conjunto de los números Reales.
Ejercicios de ecuaciones cuadráticas

1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene dos soluciones reales distintas


1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene dos soluciones reales distintas


1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos



3 La ecuación no tiene solución en los números reales

1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos



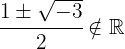
3 La ecuación no tiene solución en los números reales

1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene dos soluciones reales e iguales


1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene dos soluciones reales distintas


1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene dos soluciones reales distintas

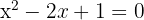
1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos


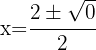


3 La ecuación tiene solamente una solución real


1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos




3 La ecuación no tiene solución en los números reales.

1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene solamente una solución real.


1 Pasamos todos los términos a un sólo miembro de la ecuación para tenerla de la forma 

2 Identificamos los valores de a, b y c

3 Sustituimos en la fórmula general y resolvemos





4 La ecuación tiene solamente una solución real.


1 Resolvemos el binomio al cuadrado

2 Pasamos todos los términos de un sólo lado y los agrupamos para escribir la ecuación en la forma 

3 Identificamos los valores de a, b y c

4 Sustituimos en la fórmula general y resolvemos
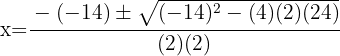




5 La ecuación tiene dos soluciones reales.


1 En este caso, podemos dividir ambos miembros de la ecuación por 7 para simplificarla

2 Identificamos los valores de a, b y c

3 Sustituimos en la fórmula general y resolvemos





4 La ecuación tiene dos soluciones reales.


1 Multiplicamos los dos miembros por −1 para obtener una ecuación equivalente con a > 0


2 La ecuación no tiene soluciones reales

1 Utilizamos la propiedad distributiva para operar el paréntesis y obtenemos:

2 Operamos y pasamos todo al primer miembro

3 Identificamos los valores de a, b y c

4 Sustituimos en la fórmula general y resolvemos





5 La ecuación tiene dos soluciones reales.


1 Identificamos los valores de a, b y c

2 Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene dos soluciones reales distintas


1 Resolvemos el binomio al cuadrado

2 Pasamos todos los términos de un sólo lado y los agrupamos para escribir la ecuación en la forma 

3 Dividimos ambos miembros de la ecuación por 2 para simplificarla

4 Identificamos los valores de a, b y c

5Sustituimos en la fórmula general y resolvemos





6 La ecuación tiene dos soluciones reales.


1 Identificamos los valores de a, b y c

2Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene dos soluciones reales distintas


1 Identificamos los valores de a, b y c

2Sustituimos en la fórmula general y resolvemos





3 La ecuación tiene dos soluciones reales distintas


1 Multiplicamos el primer miembro de la ecuación por 6, y el último por 2 para eliminar el denominador (6), y así obtenemos:

2 Identificamos los valores de a, b y c

3Sustituimos en la fórmula general y resolvemos





4 La ecuación tiene dos soluciones reales.

Recuerda que, en Superprof, también te podemos ayudar a encontrar clases de matematicas con un profesor que se pueda adaptar a tus necesidades.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Un cliente en un supermercado ha pagado un total de $312,000 por 24 L de leche 6 kg de jamón y 12 l de aceite de girasol. calcular el precio de cada artículo ,sabiendo que 6 l de aceite cuesta el doble que un jamón más 7 L de leche y que 5 kg de jamón cuesta igual que 10 l de aceite más 4 L de leche resolver esto plis es que lo es que lo he intentado resolver por todos los métodos que me han enseñado de solución como el método de cramer que tiene otro nombre pero no me lo sé como el de reducción método de eliminación método de igualación y el método gráfico
EN el ejecicio 2 esta mal resuelto el 2x de la nada se vuelve 4x ehhh… esta mal pedagogicamente formulado el ejercicio desearia ver en su totalidad que aplica
hola hay un problema, revise el artículo que se me señala y hay varios ejercicios numero 2 y no encontré el error que mencionas, podrías darme mas datos para así poder rectificar lo que esta mal, te lo agradecería mucho.
hola si la ecuación es x+1=10x+10, la respuesta es x=-1, pues si sustituyes el valor queda -1+1=10(-1)+10 o 0=-10+10, que si cumple.
Hola buenas tardes me podría decir el resultado de este ejercicio de ecuación porfavor
X+1=10x+10??
Las respuestas que diste, no me da en la ecuación