Escoge la opción correcta:
1La ecuación 
tiene...
Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
Las raíces son
La ecuación tiene dos soluciones simples que son 
y 
2La ecuación 
tiene...
Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
La ecuación tiene una solución doble que es: 
3La ecuación 
tiene...
Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
La ecuación tiene una solución doble que es: 
4La ecuación 
tiene...
Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
La ecuación no tiene soluciones reales, ya que el radicando es negativo.
5La ecuación 
tiene...
Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
Las raíces son
La ecuación tiene dos soluciones simples que son 
y 
.
6La ecuación 
tiene...
Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
La ecuación no tiene soluciones reales, ya que el radicando es negativo.
Resuelve las siguientes cuestiones:
7Calcula el valor de 
para que la ecuación 
tenga un única solución.
; 
Para que la ecuación tenga una raíz doble se debe verificar que el discriminante de la misma sea nulo.
El discriminante es 
Igualamos el discriminante a cero y despejamos
Así, cuando se tiene una raiz doble.
8Sabemos que para 
el polinomio 
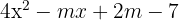tiene un raíz doble. Calcula otro valor de 
para que dicho polinomio tenga una raíz doble.
m =
Para el valor y para el valor que hayas obtenido en el apartado anterior calcula la solución de la ecuación 
 | |
 | |
Que el polinomio 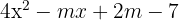tenga una raíz doble quiere decir que la ecuación tiene una única solución.
Para que la ecuación tenga una única solución se debe verificar que el discriminante sea igual a 0.
Desarrollando se obtiene la ecuación cuadrática 
Resolvemos empleando la fórmula para encontrar las raíces de la ecuación de segundo grado
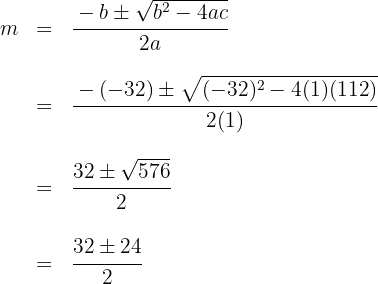
Las raíces son
Por tanto, para que el polinomio dado tenga una raíz doble deberá ser o 
Para , la ecuación se transforma en: 
Para , la ecuación se transforma en: 
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Un cliente en un supermercado ha pagado un total de $312,000 por 24 L de leche 6 kg de jamón y 12 l de aceite de girasol. calcular el precio de cada artículo ,sabiendo que 6 l de aceite cuesta el doble que un jamón más 7 L de leche y que 5 kg de jamón cuesta igual que 10 l de aceite más 4 L de leche resolver esto plis es que lo es que lo he intentado resolver por todos los métodos que me han enseñado de solución como el método de cramer que tiene otro nombre pero no me lo sé como el de reducción método de eliminación método de igualación y el método gráfico
EN el ejecicio 2 esta mal resuelto el 2x de la nada se vuelve 4x ehhh… esta mal pedagogicamente formulado el ejercicio desearia ver en su totalidad que aplica
hola hay un problema, revise el artículo que se me señala y hay varios ejercicios numero 2 y no encontré el error que mencionas, podrías darme mas datos para así poder rectificar lo que esta mal, te lo agradecería mucho.
hola si la ecuación es x+1=10x+10, la respuesta es x=-1, pues si sustituyes el valor queda -1+1=10(-1)+10 o 0=-10+10, que si cumple.
Hola buenas tardes me podría decir el resultado de este ejercicio de ecuación porfavor
X+1=10x+10??
Las respuestas que diste, no me da en la ecuación