Capítulos
Una ecuación de segundo grado es toda expresión de la forma:
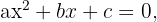 con
con 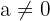

Resolución de ecuaciones de 2º grado
La ecuación de segundo grado se resuelve aplicando la siguiente fórmula:
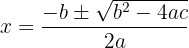
Ejemplo: Hallar las soluciones de 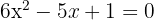
1 Primero encontramos los valores de los coeficientes
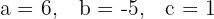
2 Sustituimos los valores en la fórmula y resolvemos

3 Observamos que se obtienen dos valores para  , estos usualmente se representan por
, estos usualmente se representan por 
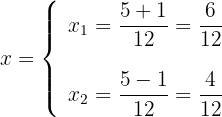
4 Simplificamos los resultados y obtenemos
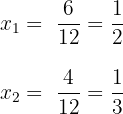
Discriminante y tipos de soluciones
El radicando de la raíz cuadrada que se encuentra en la fórmula que se emplea para resolver una ecuación de segundo grado, se conoce como discriminante
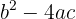
A partir del discriminante se puede conocer el tipo de soluciones de la ecuación de segundo grado
1 Si 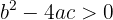 , entonces
, entonces 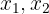 son soluciones reales y distintas.
son soluciones reales y distintas.
2 Si 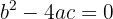 , entonces
, entonces 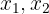 son soluciones reales e iguales.
son soluciones reales e iguales.
3 Si 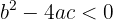 , entonces la ecuación no posee soluciones reales.
, entonces la ecuación no posee soluciones reales.
Ejemplo: Determinar los tipos de soluciones de 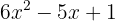
Los coeficientes son 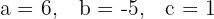
Sustituimos los valores en la fórmula y resolvemos
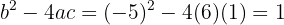
Como el discriminante es mayor que cero, entonces la ecuación de segundo grado posee dos soluciones reales y distintas.
Ejercicios de ecuaciones de 2º grado a partir de sus soluciones
Hallar las ecuaciones de segundo grado que tienen por soluciones:

1Si conocemos las raíces  de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
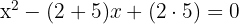
3Así, la ecuación buscada es
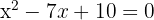

1Si conocemos las raíces  de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos

3Así, la ecuación buscada es

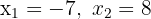
1Si conocemos las raíces 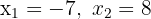 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos

3Así, la ecuación buscada es

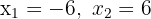
1Si conocemos las raíces 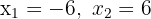 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
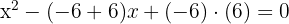
3Así, la ecuación buscada es


1Si conocemos las raíces  de la ecuación se segundo grado, podemos escribir esta como
de la ecuación se segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
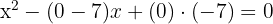
3Así, la ecuación buscada es

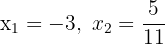
1Si conocemos las raíces 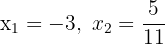 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
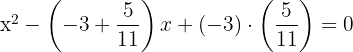
3Así, la ecuación buscada es

4La ecuación anterior se puede expresar con coeficientes enteros, para ello multiplicamos ambos lados de la ecuación por 

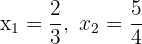
1Si conocemos las raíces 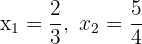 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
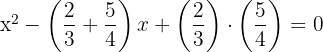
3Así, la ecuación buscada es

4La ecuación anterior se puede expresar con coeficientes enteros, para ello multiplicamos ambos lados de la ecuación por 
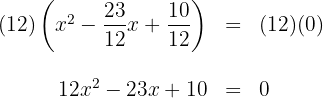
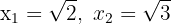
1Si conocemos las raíces 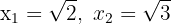 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
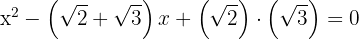
3Así, la ecuación buscada es
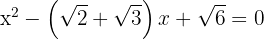
Ejercicios de factorización de ecuaciones de 2º grado
Factorizar las siguientes ecuaciones de segundo grado

1Si conocemos las raíces  de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
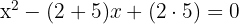
3Así, la ecuación buscada es
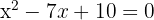

1Si conocemos las raíces  de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos

3Así, la ecuación buscada es

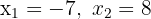
1Si conocemos las raíces 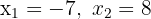 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos

3Así, la ecuación buscada es

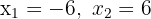
1Si conocemos las raíces 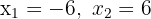 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
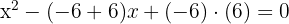
3Así, la ecuación buscada es


1Si conocemos las raíces  de la ecuación se segundo grado, podemos escribir esta como
de la ecuación se segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
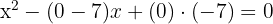
3Así, la ecuación buscada es

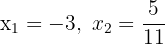
1Si conocemos las raíces 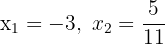 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
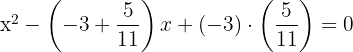
3Así, la ecuación buscada es

4La ecuación anterior se puede expresar con coeficientes enteros, para ello multiplicamos ambos lados de la ecuación por 

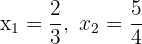
1Si conocemos las raíces 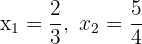 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
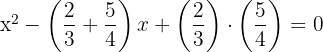
3Así, la ecuación buscada es

4La ecuación anterior se puede expresar con coeficientes enteros, para ello multiplicamos ambos lados de la ecuación por 
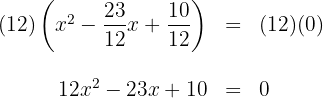
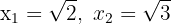
1Si conocemos las raíces 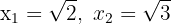 de la ecuación de segundo grado, podemos escribir esta como
de la ecuación de segundo grado, podemos escribir esta como

2Sustituimos las raíces y obtenemos
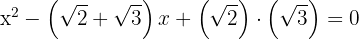
3Así, la ecuación buscada es













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
2x+y-z=-1
X-2y+z=5
3x-y-2z=0
Ecuaciones metodo Guss jordan
no entiendo deberían explicar un poco mas detallado
Hola, entendemos tu punto, pero para lograrlo podrías mencionar mas específicamente donde no entendiste y con gusto te ayudamos.
Un cliente en un supermercado ha pagado un total de $312,000 por 24 L de leche 6 kg de jamón y 12 l de aceite de girasol. calcular el precio de cada artículo ,sabiendo que 6 l de aceite cuesta el doble que un jamón más 7 L de leche y que 5 kg de jamón cuesta igual que 10 l de aceite más 4 L de leche resolver esto plis es que lo es que lo he intentado resolver por todos los métodos que me han enseñado de solución como el método de cramer que tiene otro nombre pero no me lo sé como el de reducción método de eliminación método de igualación y el método gráfico
Simplemente traspasas todo al miembro correspondiente y operas, despues traspasas el primer miembro dividiendo al segundo, lo divides y a esta
hola si la ecuación es x+1=10x+10, la respuesta es x=-1, pues si sustituyes el valor queda -1+1=10(-1)+10 o 0=-10+10, que si cumple.