Temas
Para plantear problemas sobre móviles que llevan velocidad constante se utilizan las fórmulas del movimiento rectilíneo uniforme:
espacio = velocidad × tiempo
Podemos encontrarnos con tres casos de problemas de móviles:
1. Los móviles van en sentido contrario
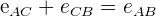
El espacio recorrido por el primero hasta el punto de encuentro más el espacio que ha recorrido el segundo es igual a la distancia que los separa
Ejemplo:
Dos ciudades 
y 
distan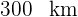 
entre sí. A las 9 de la mañana parte de la ciudad un coche hacia la ciudad con una velocidad de 
, y de la ciudad parte otro hacia la ciudad con una velocidad de 
. Hallar el tiempo que tardarán en encontrarse; la hora del encuentro; la distancia recorrida por cada uno.
El tiempo que tardarán en encontrarse
1 Conocemos para cada coche la velocidad. Sustituimos en la fórmula de espacio y obtenemos
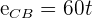
2 Sabemos que el espacio recorrido por el primer coche más el espacio recorrido por el segundo es igual a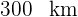
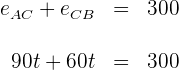
3 Resolvemos la ecuación anterior
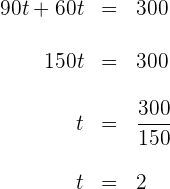
Los autos tardarán 2 horas en encontrarse.
La hora del encuentro
Se encontrarán a las 11 de la mañana porque parten a las 9 de la mañana y transcurren dos horas hasta el encuentro.
La distancia recorrida por cada coche
Para encontrar la distancia recorrida por cada coche, sustituimos el tiempo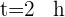 
en la fórmula de espacio recorrido
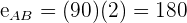
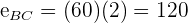
De esta forma tenemos que el primer coche recorre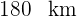 
y el segundo coche recorre 
2. Los móviles van en el mismo sentido
El espacio recorrido por el primer vehículo menos el espacio recorrido por el 2º vehículo es igual a la distancia que los separa
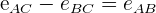
Ejemplo:
Dos ciudades y distan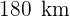 
entre sí. A las 9 de la mañana sale un coche de cada ciudad y los dos coches van en el mismo sentido. El que sale de circula a , y el que sale de va a . Hallar el tiempo que tardarán en encontrarse; la hora del encuentro; la distancia recorrida por cada uno.
El tiempo que tardarán en encontrarse
1 Conocemos para cada coche la velocidad. Sustituimos en la fórmula de espacio y obtenemos
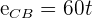
2 Sabemos que el espacio recorrido por el primer coche menos el espacio recorrido por el segundo es igual a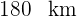
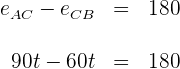
3 Resolvemos la ecuación anterior
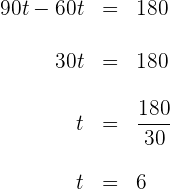
Los autos tardarán 6 horas en encontrarse.
La hora del encuentro
Se encontraran a las 3 de la tarde porque parten a las 9 de la mañana y transcurren seis horas hasta el encuentro.
La distancia recorrida por cada coche
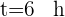en la fórmula de espacio recorrido: 
, 
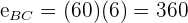. De esta forma tenemos que el primer coche recorre 
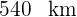y el segundo coche recorre 
3. Los móviles parten del mismo punto y con el mismo sentido
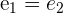
El espacio recorrido por el primer vehículo es igual al espacio recorrido por el segundo.
Ejemplo:
Un coche sale de la ciudad con velocidad de 
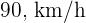. Tres horas más tarde sale de la misma ciudad otro coche en persecución del primero con una velocidad de 
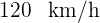. Hallar el tiempo que tardará el segundo coche en alcanzar al primero; la distancia a la que se produce el encuentro.
El tiempo que tardará el segundo coche en alcanzar al primero.
1 Si el tiempo empleado por el primer coche es 
, el del segundo que sale tres horas más tarde será 
.
Sustituimos en la fórmula de espacio y obtenemos
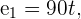
2 Sabemos que el espacio recorrido por ambos coches es el mismo
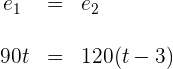
3 Resolvemos la ecuación anterior
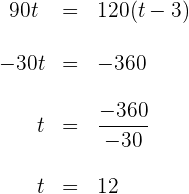
El primer coche tarda 
.
El segundo coche tarda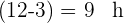 
.
La distancia a la que se produce el encuentro.
Calculamos el espacio recorrido por uno de los dos coches
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
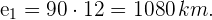
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
x²-6x+8=0
x²+6x=0-8
4x=-8
x=-8/4
x=-2
Hola Valeria, lamento la intromisión, si aún necesitas la respuesta, la ecuación es de segundo grado porque la letra x² es la de mayor exponente, debido a que no tienes término semejantes, como x+x, o x²+x² (por ejemplo) no puedes operarios de manera directa. Puedes utilizar la fórmula de segundo general de segundo grado (Que la puedes encontrar en esta página web y te explica cómo usarla, es muy sencillo) o puedes hacer una factorización, tus resultados son x=4 y x=2.
Me parece que el ultimo ejercicio (la tricuadrada) se puede hacer de otra forma ya que hace x^3=t cuando en realidad si se hace x^6=t^3 y x^3=t te da t^3-7t+6 lo cual haciendo un sencillo ruffini te da las x como resultado t=-3 t=2 y t=1 y al volver a pasarlo a las x te da como resultado x1= ∄ y x2= ∄ (al ser la raiz cuadrada de -3) , x3=raiz cuadrada +2, x4= raiz cuadrada -2, x5=+1 y x6=-1. Saludos.
Si haces x^6=t^3 te da x^2=t o x^3=t^(3/2) lo cual complica en vez de facilitar la ecuación, además de que la expresión x^3=t esta mal.
resolver la ecuacion x−4
3
− 5 = 0
X=4 yx= 2
2X=4+2
X=6/2
X=3