Señala en cada caso el número real al que corresponde la representación gráfica dada. Observa el punto gris.
1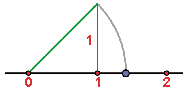
1Tomamos un cuadrado de lado 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 
2En efecto, pues 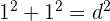 , de donde,
, de donde, 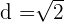
3Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro cuadrado). De este modo, representamos en la recta real el número 
2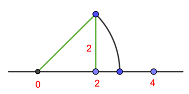
1Tomamos un cuadrado de lado 2. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 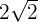
2En efecto, pues  , de donde,
, de donde, 
3Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro cuadrado). De este modo, representamos en la recta real el número 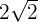
3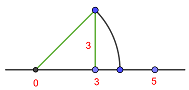
1Tomamos un cuadrado de lado 3. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 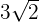
2En efecto, pues 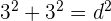 , de donde,
, de donde, 
3Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro cuadrado). De este modo, representamos en la recta real el número 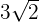
4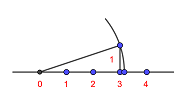
1Tomamos un rectángulo de base 3 y altura 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 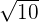
2En efecto, pues 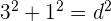 , de donde,
, de donde, 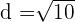
3Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro rectángulo). De este modo, representamos en la recta real el número 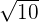
5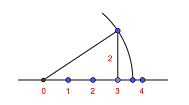
1Tomamos un rectángulo de base 3 y altura 2. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 
2En efecto, pues 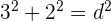 , de donde,
, de donde, 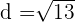
3Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro rectángulo). De este modo, representamos en la recta real el número 
6
1Tomamos un rectángulo de lado 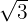 y altura 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide
y altura 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 
2En efecto, pues  , de donde,
, de donde, 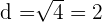
3Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro rectángulo). De este modo, representamos en la recta real el número 
7
1Tomamos un rectángulo de base 4 y lado 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 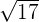
2En efecto, pues 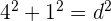 , de donde,
, de donde, 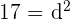 y, por tanto,
y, por tanto, 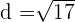
3Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro cuadrado). De este modo, representamos en la recta real el número 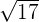
8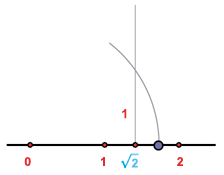
1Tomamos un rectángulo de base  y de altura 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide
y de altura 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 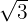
2En efecto, pues 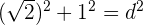 , de donde,
, de donde, 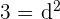 y, por tanto,
y, por tanto, 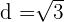
3Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro cuadrado). De este modo, representamos en la recta real el número 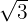
9
1En primer lugar representamos el número 
2Para ello tomamos un rectángulo de base 2 y altura 1. Entonces, usando el teorema de Pitágoras sabemos que su diagonal mide 
3En efecto, pues 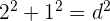 , de donde,
, de donde, 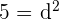 y, por tanto,
y, por tanto, 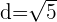
4Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro cuadrado). De este modo, representamos en la recta real el número 

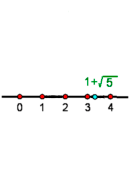
5Ahora representamos el número  , para lo que basta sumar una unidad
, para lo que basta sumar una unidad  . Esto se hace transportando con el compás cualquier unidad, por ejemplo, la tomada pinchando en 0 y abriendo hasta 1.
. Esto se hace transportando con el compás cualquier unidad, por ejemplo, la tomada pinchando en 0 y abriendo hasta 1.
6Por último, debemos encontrar la mitad del valor obtenido anteriormente. Para ello trazamos la mediatriz del segmento determinado por 0 y por 
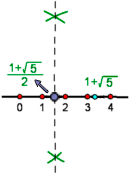
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
porque surge una fraccion mixta del caso uno ejemplo 2 alguien me podria explicar
Me aparecen desigualdades en el ejemplo que mencionas y ninguna fracción.
Tengo aquí una duda
Sabemos que no existen raíces de negativos, solo en los complejos
Entonces supongamos que estamos en los complejos y no en los reales la propiedad de la multiplicacion de radicales se cumple? Lo comento porque en lo
Raíz de (-4) × raíz de (-9)
Si lo hacemos por separado da – 6
Pues obtenemos (2i)(3i)
Pero si aplicamos la propiedad da como resultado 6
Cuál es la correcta?
Si se multiplica 2i x 3 i se obtiene 6 i^2, pero i^2 = -1
Entonces el resultado es – 6
Si te refieres al ejercicio |x-2|>=1, el resultado es correcto el método puede no ser claro.
Se recomienda tomar por casos, a) x-2>=1 y b) x-2<=-1 se resuelve cada uno y el resultado concuerda con lo mostrado.
En el ejercicio 3 no me aparece ningún 24 y 8.