Números reales. Resumen II
Los números irracionales
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es 
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
Los números reales
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por 
.
Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.
Operaciones con números reales
Suma
Propiedades
1.Interna:
a + b 
2.Asociativa:
(a + b) + c = a + (b + c) ·
3.Conmutativa:
a + b = b + a
4.Elemento neutro:
a + 0 = a
5.Elemento opuesto
Dos números son opuestos si al sumarlos obtenemos como resultado el cero.
El opuesto del opuesto de un número es igual al mismo número.
la diferencia de dos números reales se define como la suma del minuendo más el opuesto del sustraendo.
a - b = a + (- b)
Producto
Propiedades
1.Interna:
a · b
2.Asociativa:
(a · b) · c = a · (b · c)
3.Conmutativa:
a · b = b · a
4. Elemento neutro:
a ·1 = a
5. Elemento inverso:
Un número es inverso del otro si al multiplicarlos obtenemos como resultado el elemento unidad.
6.Distributiva:
a · (b + c) = a · b + a · c
7.Sacar factor común:
a · b + a · c = a · (b + c)
La división de dos números reales se define como el producto del dividendo por el inverso del divisor.
Intervalos
Los intervalos están determinados por dos números que se llaman extremos. En un intervalo se encuentran todos los números comprendidos entre ambos y también pueden estar los extremos.
Intervalo abierto
(a, b) = {x / a < x < b}
Intervalo cerrado
[a, b] = {x / a ≤ x ≤ b}
Intervalo semiabierto por la izquierda
(a, b] = {x / a < x ≤ b}
Intervalo semiabierto por la derecha
[a, b) = {x / a ≤ x < b}
Semirrectas
x > a
(a, +∞) = {x / a < x < +∞}
x ≥ a
[a, +∞) = {x / a ≤ x < +∞}
x < a
(-∞, a) = {x / -∞ < x < a}
x ≤ a
(-∞, a] = {x / -∞ < x ≤ a}
Valor absoluto
Valor absoluto de un número real a, se escribe |a|, es el mismo número a cuando es positivo o cero, y opuesto de a, si a es negativo.
Propiedades
|a| = |−a|
|a · b| = |a| ·|b|
|a + b| ≤ |a| + |b|
Distancia
La distancia entre dos números reales a y b, que se escribe d(a, b), se define como el valor absoluto de la diferencia de ambos números:
d(a, b) = |b − a|
Entornos
Se llama entorno de centro a y radio r, y se denota por Er(a) o E(a,r), al intervalo abierto (a-r, a+r).
Er(a) = (a-r, a+r)
Entornos laterales:
Por la izquierda
Er(a-) = (a-r, a)
Por la derecha
Er(a+) = (a, a+r)
Entorno reducido
E r*(a) = { x (a-r, a+r), x ≠ a}
Potencias
Con exponente entero
Con exponente racional
Propiedades
1.a0 = 1 ·
2.a1 = a
3.am · a n = am+n
4.am : a n = am - n
5.(am)n=am · n
6.an · b n = (a · b) n
7.an : b n = (a : b) n
Radicales
Un radical es una expresión de la forma 
, en la que n 
y a ; con tal que cuando a sea negativo, n ha de ser impar.
Se puede expresar un radical en forma de potencia:
Radiales equivalentes
Si se multiplican o dividen el índice y el exponente de un radical por un mismo número natural, se obtiene otro radical equivalente.
Simplificación de radicales
Si existe un número natural que divida al índice y al exponente (o los exponentes) del radicando, se obtiene un radical equivalente.
Reducción de radicales a índice común
1Hallamos el mínimo común múltiplo de los índices, que será el común índice
2Dividimos el común índice por cada uno de los índices y cada resultado obtenido se multiplica por sus exponentes correspondientes.
Extracción de factores fuera del signo radical
Se descompone el radicando en factores. Si:
Un exponente es menor que el índice, el factor correspondiente se deja en el radicando.
Un exponente es igual al índice, el factor correspondiente sale fuera del radicando.
Un exponente es mayor que el índice, se divide dicho exponente por el índice. El cociente obtenido es el exponente del factor fuera del radicando y el resto es el exponente del factor dentro del radicando.
Introducción de factores dentro del signo radical
Se introduce los factores elevados al índice correspondiente del radical.
Operaciones con radicales
Suma de radicales
Solamente pueden sumarse (o restarse) dos radicales cuando son radicales semejantes, es decir, si son radicales con el mismo índice e igual radicando.
Producto de radicales
Radicales del mismo índice
Para multiplicar radicales con el mismo índice se multiplican los radicandos y se deja el mismo índice.
Radicales de distinto índice
Primero se reducen a índice común y luego se multiplican.
Cociente de radicales
Radicales del mismo índice
Para dividir radicales con el mismo índice se dividen los radicandos y se deja el mismo índice.
Radicales de distinto índice
Primero se reducen a índice común y luego se dividen.
Potencia de radicales
Para elevar un radical a una potencia se eleva a dicha potencia el radicando y se deja el mismo índice.
Raíz de un radical
La raíz de un radical es otro radical de igual radicando y cuyo índice es el producto de los dos índices.
Racionalizar
Consiste en quitar los radicales del denominador, lo que permite facilitar el cálculo de operaciones como la suma de fracciones.
Podemos distinguir tres casos.
1Del tipo 
Se multiplica el numerador y el denominador por 
.
2Del tipo 
Se multiplica numerador y denominador por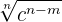 
.
3Del tipo 
, y en general cuando el denominador sea un binomio con al menos un radical.
Se multiplica el numerador y denominador por el conjugado del denominador.
Logaritmos
El logaritmo de un número, en una base dada, es el exponente al cual se debe elevar la base para obtener el número.
Siendo a la base, x el número e y el logaritmo.
De la definición de logaritmo podemos deducir:
Propiedades de los logaritmos:
Logaritmos decimales:
Son los de base 10. Se representan por log (x).
Logaritmos neperianos:
Son los que tienen base e. Se representan por ln (x) o L(x).
