Temas
Pasos para multiplicar números racionales
1 Obtenemos el numerador por el producto de los numeradores.
2 Obtenemos el denominador por el producto de los denominadores.
Ejemplo:
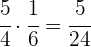
Propiedades de la multiplicación de números racionales
Interna
El resultado de multiplicar dos números racionales es otro número racional.
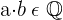
Propiedad asociativa
El modo de agrupar los factores no varía el resultado.
Ejemplo:
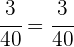
Propiedad conmutativa
El orden de los factores no varía el producto.
Ejemplo
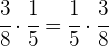
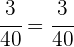
Elemento neutro
El 
es el elemento neutro de la multiplicación, porque todo número multiplicado por él da el mismo número.
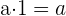
Ejemplo
Elemento inverso
Un número es inverso de otro si al multiplicarlos obtenemos como resultado el elemento unidad.
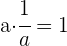
Ejemplo
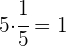
Propiedad distributiva
El producto de un número por una suma es igual a la suma de los productos de dicho número por cada uno de los sumandos.
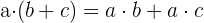
Ejemplo
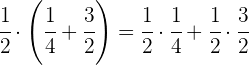
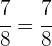
Sacar factor común
Es el proceso inverso a la propiedad distributiva.
Si varios sumandos tienen un factor común, podemos transformar la suma en producto extrayendo dicho factor.
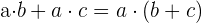
Ejemplo
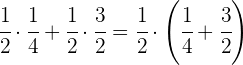
División de números racionales
La división de dos números racionales es otro número racional que tiene:
Por numerador el producto de los extremos.
Por denominador el producto de los medios.
También podemos definir la división de dos números racionales como producto del primero por el inverso del segundo.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hallar la fracción generatriz de los siguientes números decimales con periodo mixto
1)7,623
2)7,623
3)7623
4)*)4,165
5555(234:53-78×5)+66666:66(446-55×4)×56
Quien me ayuda??
14+ (3+8+5):2: [4+/32-20):4] = ayudaaa
operaciones con fracciones con 3 fracciones con estos numeros 10/3+ 1/5 + 3/2
[-2+×(2-5)÷3]- [(3-5-2)-2×(3-4)]
pero la 3 esta mal
Si te refieres al ejercicio de los autos no esta mal pues compara dos fracciones 5/11 y 6/13 calcula minimo comun multiplo de 11 y 13, que es 143 y cada fracción la convierte a cientocuarentatresavos y compara.