Temas
Los números enteros 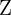 es el conjunto de números conformado por los naturales (también denominados enteros positivos), sus opuestos (enteros negativos) y el cero. Los números enteros son del tipo:
es el conjunto de números conformado por los naturales (también denominados enteros positivos), sus opuestos (enteros negativos) y el cero. Los números enteros son del tipo:
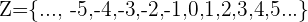

Orden de los números enteros
Los números enteros están ordenados de forma ascendente. Los criterios para determinar el orden de un subconjunto de número enteros es el siguiente:
1 Todo número negativo es menor que cero. Es decir, si  es un entero negativo entonces
es un entero negativo entonces  .
.
2 Todo número positivo es mayor que cero. Es decir, si  es un entero positivo entonces
es un entero positivo entonces  .
.
3 De dos enteros positivos es mayor el que tiene mayor valor absoluto. Es decir, si  y
y  son enteros positivos que satisfacen que
son enteros positivos que satisfacen que  entonces
entonces 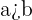 .
.
Por ejemplo,  lo que significa que
lo que significa que 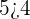 .
.
4 De dos enteros negativos es mayor el que tiene menor valor absoluto. Es decir, si  y
y  son enteros negativos que satisfacen que
son enteros negativos que satisfacen que  entonces
entonces 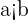 .
.
Por ejemplo, 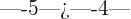 lo que significa que
lo que significa que  . Gráficamente, entre más a la derecha esté un número, en la recta numérica, mayor será.
. Gráficamente, entre más a la derecha esté un número, en la recta numérica, mayor será.
Suma de números enteros
1 Si los sumandos son del mismo signo, se suman los valores absolutos y al resultado se le pone el signo común.
Por ejemplo,  y
y  tienen el mismo signo por lo cual se calcula la suma de sus valores absolutos y se le asigna el signo de ambos números es decir
tienen el mismo signo por lo cual se calcula la suma de sus valores absolutos y se le asigna el signo de ambos números es decir 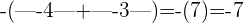 .
.
2 Si los sumandos son de signo distinto, se restan los valores absolutos (al mayor le restamos el menor) y al resultado se le pone el signo del número de mayor valor absoluto.
Por ejemplo,  y
y  tienen diferente signo por lo cual se calcula la resta de sus valores absolutos y se le asigna el signo del número de mayor valor absoluto, es decir:
tienen diferente signo por lo cual se calcula la resta de sus valores absolutos y se le asigna el signo del número de mayor valor absoluto, es decir:  (recordemos que asignamos el número negativo pues
(recordemos que asignamos el número negativo pues  ).
).
Propiedades de la suma
Si 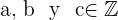 entonces se satisfacen las siguientes propiedades:
entonces se satisfacen las siguientes propiedades:
1. Interna:

2. Asociativa:
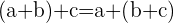
3. Conmutativa:

4. Elemento neutro:
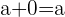
5. Elemento inverso aditivo
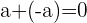
¿Buscas un/a profe mates? No te compliques: ¡encuéntral@ en Superprof!
Diferencia de números enteros
La resta de los números enteros se obtiene sumando al minuendo el opuesto del sustraendo.

Propiedades de la resta
1. Interna:
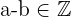
2. No es Conmutativa:
Notemos que 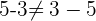
Multiplicación de números enteros
El producto de varios números enteros es otro número entero, que tiene como valor absoluto el producto de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
Regla de los signos
- El producto de la multiplicación de dos números con el mismo signo siempre es positiva:
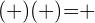
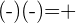
- El producto de la multiplicación de dos números con diferente signo siempre es negativa:

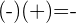
Propiedades de la multiplicación
1. Interna:

2. Asociativa:
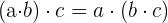
3. Conmutativa:
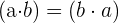
4. Elemento neutro multiplicativo:
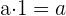
5. Distributiva:

6. Sacar factor común:
Es el proceso inverso a la propiedad distributiva.
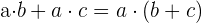
Cociente de números enteros
El cociente de dos números enteros es otro número, que tiene como valor absoluto el cociente de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
Propiedades del cociente
1. No es una operación interna:
Notemos que 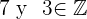 pero
pero  no es un número entero.
no es un número entero.
2. No es Conmutativo.
Potencias con exponente entero
Si tenemos que el exponente es un número natural  , entonces este indica las veces que aparece la base
, entonces este indica las veces que aparece la base  multiplicando por si mismo, por ejemplo
multiplicando por si mismo, por ejemplo

Regla de los signos de potencias
- Los números positivos elevados a cualquier potencia son siempre positivos:

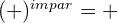
- Si un número es negativo y se eleva a una potencia el signo del valor resultante depende de si la potencia es par o impar:
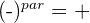

Propiedades de las potencias
1. Números elevados a potencia cero:
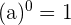 ·
·
2. Números elevados a la potencia 1:
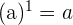
3. Producto de potencias con la misma base:
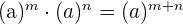 .
.
4. División de potencias con la misma base:

5. Potencia de una potencia:

6. Producto de potencias con el mismo exponente:
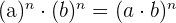 .
.
7. Cociente de potencias con el mismo exponente:
 .
.
8. Potencias de exponente entero negativo
Las potencias de exponente negativo se denotan como:

En general, las potencias de exponentes negativos no dan como resultado un número entero.
Radicales
Un radical es una expresión de la forma  , donde
, donde  y
y  . Ademas
. Ademas  es llamada radicando y
es llamada radicando y  índice. Para que la operación sea valida en los reales si
índice. Para que la operación sea valida en los reales si  es negativo,
es negativo,  debe ser impar. En general, la raíz de un número natural no es un número entero.
debe ser impar. En general, la raíz de un número natural no es un número entero.
Raíz cuadrada de un cuadrado perfecto
La raíz cuadrada es la operación inversa a elevar al cuadrado. La raíz cuadrada de un número natural es exacta, siempre que el radicando sea un cuadrado perfecto (un número es un cuadrado perfecto si cuando se descompone en sus factores primos, cada uno de los términos está elevado a una potencia par).
Algunos ejemplos son:
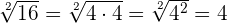
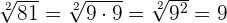
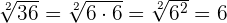
Jerarquía de operaciones
Cuando se realizan un conjunto de operaciones simultaneas es necesaria tener en consideración la jerarquía de las operaciones que se presentan a continuación:
1 Efectuar las operaciones entre paréntesis, corchetes y llaves.
2 Calcular las potencias y raíces.
3 Efectuar los productos y cocientes.
4 Realizar las sumas y restas.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Una pregunta que se tiene en 0+7?
Simplificar:
(-12)-(-7)-[(+12)-(+7)-(-5)]-(+12)-(+18)
-12+7-12-7+5-12-18
-49
Ese es el resultado
Necesito ayuda para 5ejemplos relacionados con números enteros y su respectiva solucion
Es menor porque todos saben que los números enteros positivos simpre pero siempre seran mayores que cualquier otro número negativo
es mayor
30 es majur que 25