Temas
La divisibilidad es un concepto fundamental en matemáticas que nos permite comprender cómo los números se relacionan entre sí. Nos permite determinar si un número es divisible por otro sin necesidad de realizar divisiones exactas.
A través de la práctica y la comprensión de las reglas de divisibilidad, podrás desarrollar habilidades para simplificar cálculos, factorizar números y resolver una amplia gama de problemas matemáticos.

Números primos y compuestos
 es menor a 800, pero
es menor a 800, pero  es mayor a 800. Si realizamos la multiplicación nos da
es mayor a 800. Si realizamos la multiplicación nos da 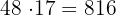
Luego, considerando los enteros siguientes al 48, tenemos
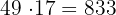

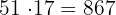
Observemos que 867 ya es mayor a 860. Por lo tanto, el resultado es: 816, 833, 850
- Los números 848 y 3566 son compuestos porque, al acabar en cifra par, son divisibles por dos.
- El número 7287 también es compuesto porque es divisible entre 3, esto lo sabemos porque la suma de sus digitos es divisible entre 3.
- El número 179 es primo porque no es divisible entre 2, 3, 5, 7, 11. Vamos a probar dividiendo por 13:
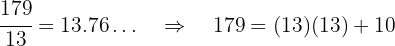
Como la división no es exacta y el cociente es igual al divisor, entonces el número es primo.
- El número 311 es primo porque no es divisible entre 2, 3, 5, 7, 11. Probaremos dividiendo por 13:

podemos continuar y vemos que la división no es exacta hasta 311, por lo tanto número primo.
3 Calcula, mediante una tabla, todos los números primos comprendidos entre 400 y 450.
| 401 | 409 | ||||||||
| 419 | |||||||||
| 421 | |||||||||
| 431 | 433 | 439 | |||||||
| 443 | 449 |
Números primos: 401, 409, 419, 421, 431, 433, 439, 443, 449
Factorización
4 Haz la descomposición en factores de los siguientes números:
- 216
- 360
- 432
Hacemos la descomposición en números primos comenzando con el 2, si no se puede 3, luego 5, y así sucesivamente

entonces

2 360:

entonces
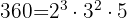
3 432:

entonces
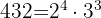
5 Factoriza 342 y calcula su número de divisores.

es decir,
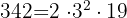
Sumamos la unidad a cada uno de los exponentes de los factores de 342. Luego multiplicamos los resultados obtenidos, entonces,
Número de factores:
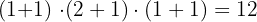
6 Haz la descomposición de factores de:
- 2250
- 3500
- 2520
Similar a uno de los ejercicios anteriores

por tanto
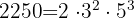
2 3500:

por lo tanto
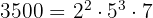
3 2520:

por tanto
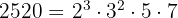
Máximo común divisor, mínimo común múltiplo y algoritmo de Euclides
7 Calcula el máximo común divisor (m.c.d.) y mínimo común múltiplo (m.c.m.) de:
- 428 y 376
- 148 y 156
- 600 y 1 000
En primer lugar descomponemos en factores,

es decir 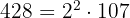 y
y

es decir, 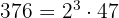 . Para hallar el m.c.d. tomamos los factores comunes de menor exponente
. Para hallar el m.c.d. tomamos los factores comunes de menor exponente
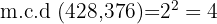
Para hallar el m.c.m. tomamos los factores comunes y no comunes de mayor exponente
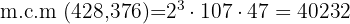
2 148 y 156:
Descomponemos en factores

y

entonces
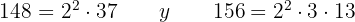
Calculamos m.c.m y m.c.d :

3 600 y 1000 : Nuevamente, comenzamos descomponiendo en factores

es decir 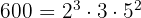 y
y

es decir 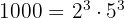 . Ya con los factores obtenemos que el m.c.d es
. Ya con los factores obtenemos que el m.c.d es
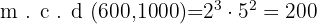
y el m.c.m
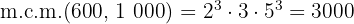
8 Calcula el m. c. d. y m.c.m. de:
- 72, 108 y 60
- 1048, 786 y 3930
Descomponemos en factores y obtenemos que

Para hallar el m.c.d. tomamos los factores comunes de menor exponente
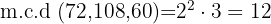
Para hallar el m.c.m. tomamos los factores comunes y no comunes de mayor exponente
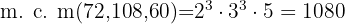
2 1048, 786 y 3930:
Nuevamente descomponemos en factores y obtenemos que

entonces

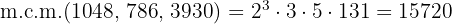
9 Calcula, utilizando el algoritmo de Euclides, el m.c.d. de:
- 72 y 16
- 656 y 848
- 1278 y 842
Primero dividimos el mayor (72) entre el menor (16), si no hay residuo 16 es la maxima medida comun, en este caso obtenemos que

es decir obtenemos un resto de 8, por lo tanto repetimos el proceso y dividimos el divisor(16) entre el residuo(8), y si es exacto, entonces 8 es la maxima medida comun. Notemos que
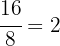
por lo tanto, 8 es el m.c.d.
2 656 y 848:
Repitiendo el proceso anterior, tendremos que la división entre 848 y 656 no es exacta, dividimos el divisor (656) entre el resto obtenido (192).
Puesto que esta división tampoco es exacta tenemos que dividir el divisor (80) entre el resto (32). Pero esta división tampoco es exacta. Ahora dividimos el divisor (32) entre el resto (16)

Como la división es exacta el m.c.d. es el divisor de esta última división: 16.
3 1278 y 842:
Primero dividimos el mayor (1278) entre el menor (842), si no hay residuo 842 es la maxima medida comun, en este caso obtenemos que
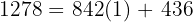
es decir obtenemos un resto de 436, por lo tanto repetimos el proceso y dividimos el divisor(842) entre el residuo(436), obteniendo

es decir obtenemos un resto de 406, por lo tanto repetimos el proceso y dividimos el divisor(436) entre el residuo(406), donde obtenemos un residuo de 30 por lo que es necesario repetir el proceso, esta vez 406 entre el residuo 30 y nuevamente no es exacto, en este caso tenemos que
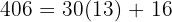
es decir, el residuo es de 16 y hacemos otro vez el proceso con 30 y 16, el cual no es exacto y se obtiene un residuo de 14. Utilizando el divisor 16 y residuo 14 checamos si la division es exacta y comprobamos que obtenemos un residuo de 2, es decir 14 no es el m.c.d, procedemos con el 14 y el 2 de donde
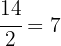
al obtener un resultado exacto se concluye que m.c.d(1278,842) = 2 .
¿Vives en la capital andaluza? ¡Échales un ojo a nuestras clases particulares matematicas Sevilla!













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
exelente!! te comento que existe otra forma de determinar si un numeros primos. segun un Argentino:
Frecuencia de Distribución de los Números Primos
La frecuencia se plantearía con una constante inicial K que consiste en exponer la base de los primos ( 2, 3, 5, 7), que se caracteriza por ser única en su orden y no repetida dentro de la frecuencia, y teniendo en cuenta que los 10 primeros dígitos se criban con el numero (2), es decir se tachan todos los divisibles exactamente por el dos. Seguido a esta constante tenemos los números primos en un cuadrante formado por 11, 13, 17, 19, 23, 29, 31, 37- espacio-41, 43, 47, 49, 53, 59, 61, 69… dentro de una frecuencia numérica con un espaciado de 30 números, que se criba por los números múltiplos dentro de su misma frecuencia. Representando la criba de Eratóstenes de manera optimizada, con una multiplicidad de los números a cribar mas clara y sustancialmente reducida en la forma de evaluar, si es primo o no un numero. (Ver Tabla 2)
El procedimiento consiste en tachar los múltiplos de los números dentro de la frecuencia a partir del número (7,11,13…) y sus sucesivos, y esto dentro de la misma frecuencia valga la redundancia, que como consecuencia resultara en un número dentro de la misma frecuencia y nunca fuera de esta, convirtiendo dicho resultado en un número no primo o compuesto, y la posición que ocupe dicho resultado dentro de la frecuencia será no primo hasta el infinito con un espació dentro de los sudcuadrantes del mismo tamaño que su múltiplo menor que lo genero, como ejemplo tenemos 7×7 que es 49 y después de un espacio de cada 7 dígitos dentro de la frecuencia tenemos el múltiplo 7×37 que es 259, ocupando un espacio así de cada siete espació hasta el infinito, y será lo mismo para cada resultado de los múltiplo dentro de esta frecuencia evaluada.
Criba por la no divisibilidad de los primos
La criba por la no divisibilidad de los primos es un procedimiento que permite hallar todos los números primos menores que un número dado. Esta consiste en formar una tabla con todos los números naturales impares con el criterio de (Frecuencia de Distribución de los Números Primos) planteada con anterioridad donde los primordiales son “11, 13, 17, 19, 23, 29, 31, 37 sumándole 30 a cada digito para secuenciar”, tal frecuencia comprendida después de la constante K (2, 3, 5, 7), es partir de 11 y n dado, que se van tachando los números que no son primos de la siguiente manera: primero se tantea hasta encontrar el numero dentro de la frecuencia que al cuadrado no rebase en valor de n, convirtiéndose en nuestro límite para cribar. Luego comenzando por el 7, se tachan todos sus múltiplos dentro de la frecuencia por la misma frecuencia; comenzando de nuevo cuando se encuentra un número entero mayor a n dado, y continuamos con el seguido número al 7 dentro de la frecuencia que es el 11, y se procede a tachar todos sus múltiplos, así sucesivamente. El proceso termina cuando el siguiente número confirmado para cribar es nuestro número planteado como límite, este se cribara pero se terminara el proceso con él.
Muy buenos ejercicios, sigue así
EXELENTE TRABAJO
El m.c.m de 20,27 y 25
Estos ejercicios me han servido mucho y vienen muy bien explicados
Calcula el mayor divisor comun de 65 ×20 y 130×30
Dos hermanos van desde su casa hasta la tienda para comprar golosinas. uno de ellos, pablo, va cada 8 minutos, el otro, Benjamín, hace su trayecto cada 12 minutos. Coincidieron cuando eran las 10 horas y 8 minutos. ¿Cada cuánto tiempo volverán a coincidir?
un alumno encontro la respuesta a su tarea en esta pagina,gracias
Dos hermanos van desde su casa hasta la tienda para comprar golosinas, uno de ellos, pablo, va cada 8 minutos, el otro, Benjamín, hace su trayecto cada 12 minutos. Coincidieron cuando eran las 10 horas y 8 minutos. ¿Cada cuánto tiempo volverán a coincidir?
Mcm=8×3=24.min. 24+8=32min
10:32min