Temas

Los/las mejores profesores/as de Matemáticas que están disponibles
Módulo de un número complejo
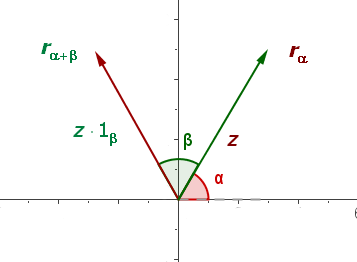
El módulo de un número complejo es el módulo del vector determinado por el origen de coordenadas y su afijo. Se designa por 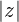 .
.
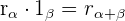
Argumento de un número complejo
El argumento de un número complejo es el ángulo que forma el vector con el eje real. Se designa por 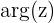 .
.
Para calcular el argumento, calculamos el  prescisdiendo de los signos, para ubicar el cuadrante en que se encuentra tendremos en cuenta:
prescisdiendo de los signos, para ubicar el cuadrante en que se encuentra tendremos en cuenta:
Expresión de un número complejo en forma polar
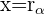
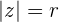 (
( es el módulo)
es el módulo)
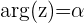 (
( es el argumento)
es el argumento)
Ejemplos de conversión de la forma polar a la forma binómica:

Para pasar de la forma polar a la binómica, tenemos que pasar en primer lugar a la forma trigonométrica:

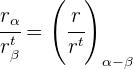
Reales e imaginarios puros de módulo unidad:


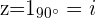

Ejemplos de pasar a la forma polar
1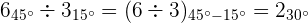
2
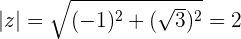


3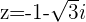

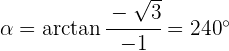
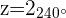
4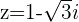
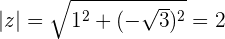
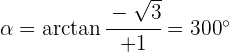

5
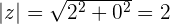
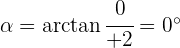
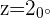
6
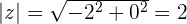


7

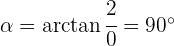
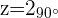
8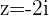

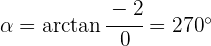
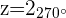













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola. ¿Me podrían ayudar con el siguiente ejercicio de números complejos?: “si dividimos un numero complejo z= a + bi entre su conjugado, obtenemos su opuesto mas 1+2i. ¿de que numero z se trata?”
Raíz sexta de menos 625
Quiero pasar -4 + 2i a forma trigonométrica y con procedimiento
¿ cómo graficar P( -3, 60°, 30°) ?
podrian resolver este ejercicio paso a paso por favor!
(-√3 + i)⁸
Z= 59049 300° Hallar y Escribir en forma polar la quinta y la novena raíz de
10 Z
Es necesario hallar una por una las potencias para calcular i1000
Si te refieres a i elevado a la 1000, no.
Primero calculas i a las potencias 0,1,2 y 3, después el 100 lo divides entre 4 y lo que quede de residuo lo usas de potencia de i y ese es el resultado.
Sea el o los números complejos z = y ||z|| = √13, el o los valores de x es/son:
•5
•+-5
•12
•+-12