In this article, we will discuss how to evaluate a given function if its limit approaches to infinity and we get an indeterminate form of infinity minus infinity. But before discussing this, first, we will see what is meant by limit of a function and l'Hôpital's Rule because both these concepts are closely related to our topic.
What is Limit?
Limit tells us how a function acts when its independent variable, i.e. x, approaches to a specific number. The formal definition of the limit concept is given below:
Consider a function (f) defined on some open interval that has a number a, except at "a" itself. We can say that the limit of f(x) as x approaches to a is L, and we can write it mathematically like this:
\lim_ {x\rightarrow a} f(x) = L
If for every number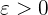 
, there is a corresponding number 
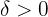in such as way that:
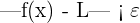
whenever:
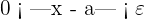
l'Hôpital's Rule
Suppose the functions f and g are differentiable, with g'(x) not zero in an interval around a, except a itself. In such a situation, one of the following points must be true:
- The limits of both the functions f(x) and g(x) are zero as x approaches a
- The functions f(x) and g(x) have infinite limit (positive or negative) as x approaches a
When one of the above discussed points are true, then the limit of the ratio of f and g, i.e.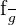 
is equal to the limit of the ratio of the differentials of the functions f ' and g ', i.e., 
{where the prime represents the appropriate derivative}, until the limit exists, or is infinite.
l'Hôpital's Rule can be applied in one of the following forms of the limit:
, where both f(x) and g(x) approach to 0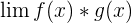
, where f(x) approaches to infinity and g(x) approaches to 0
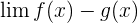, where both f(x) and g(x) approach infinity- , where both f(x) and g(x) approach to infinity
, where both f(x) and g(x) approach to 0- , where f(x) approaches 1 and g(x) approaches infinity
- , where f(x) approaches to infinity and g(x) approaches to 0
In this article, we will specifically discuss how to apply the l'Hôpital's Rule when we have the indeterminate form 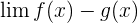, where both the functions f(x) and g(x) approach to infinity.
Example 1
Evaluate \lim_{x \rightarrow \infty} (\sqrt{x^2 - 1} - x).
Solution
The above function has an indeterminate form of 
because \lim_ {x \rightarrow \infty}(\sqrt{x^2 - 1}) is equal to 
, and \lim_ {x \rightarrow \infty} x is also equal to .
So, we will first convert the function into another indeterminate form for using the l'Hôpital's Rule. One method to convert it into another form is factoring the largest term as shown below:
When we will apply the limit on the above function as shown below, we will still get an indeterminate form of 
.
=\lim_{x \rightarrow \infty}x [\sqrt{1 - \frac{1}{x^2}} - 1]
Now, we will convert the above expression into a quotient form like this:
=\lim_{x \rightarrow \infty}\frac {\sqrt{1 - \frac{1}{x^2}}- 1}{\frac{1}{x}}
Now, will apply l'Hôpital's Rule here. To apply the l'Hôpital's Rule, we will take the first derivative of numerator and denominator separately. The first derivative of 
is 
and the derivative of 
is 
. Now, substitute these derivatives in the function like this:
=\lim_{x \rightarrow \infty}\frac {\frac{1}{\sqrt{1 - \frac{1}{x^2}}x^3}} {- \frac{1}{x^2}}
Applying the limit will give us the following answer:
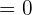
Example 2
Evaluate \lim_{x \rightarrow \infty} (\sqrt{x^2 + 5x} - x).
Solution
The above function has an indeterminate form of because \lim_ {x \rightarrow \infty}(\sqrt{x^2 + 5x}) is equal to , and \lim_ {x \rightarrow \infty} x is also equal to .
So, we will first convert the function into another indeterminate form in order to use the l'Hôpital's Rule. One method to convert it into another form is factoring the largest term as shown below:
When we will apply the limit on the above function as shown below, we will still get an indeterminate form:
=\lim_{x \rightarrow \infty}x [\sqrt{1 + \frac{5x}{x^2}} - 1]
Now, we will convert the above expression into a quotient form like this:
=\lim_{x \rightarrow \infty}\frac {\sqrt{1 + \frac{5x}{x^2}} - 1}{\frac{1}{x}}
Now, will apply l'Hôpital's Rule here. To apply the l'Hôpital's Rule, we will take the first derivative of numerator and denominator separately. The first derivative of 
is 
and the derivative of 
is . Now, substitute these derivatives in the function like this:
=\lim_{x \rightarrow \infty} -\frac {\frac{5}{2\sqrt{\frac{5}{x} +1} x^2}} {\frac{1}{x^2}}
Applying the limit (x approaches to infinity) will give us the following answer:
We can also use conjugate to evaluate such indeterminate function. In the next two examples, we will use the conjugate method to evaluate the given functions.
Example 3
Evaluate \lim_{x \rightarrow \infty} (\sqrt{x^2 + 3x} - x).
Solution
The above function has an indeterminate form of because \lim_ {x \rightarrow \infty} (\sqrt{x^2 + 3x} is equal to , and \lim_ {x \rightarrow \infty} x is also equal to .
We will use the conjugate of the function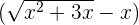 
to evaluate the function. The conjugate of 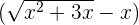is 
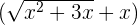. Multiply and divide the original function by this conjugate as shown below:
=\lim_{x \rightarrow \infty} (\sqrt{x^2 + 3x} - x) \cdot \frac {\sqrt{x^2 + 3x} + x} {\sqrt{x^2 + 3x} + x}
=\lim_{x \rightarrow \infty} (\sqrt{x^2 + 3x} - x) \cdot \frac {\sqrt{x^2 + 3x} + x} {\sqrt{x^2 + 3x} + x}
=\lim_{x \rightarrow \infty} \frac{(\sqrt{x^2 + 3x} - x)^2} {\sqrt{x^2 + 3x} + x}
=\lim_{x \rightarrow \infty} \frac{3x} {\sqrt{x^2 + 3x} + x}
Now, we will factor out the biggest term in the denominator and write the expression like this:
=\lim_{x \rightarrow \infty} \frac{3x} {\sqrt {x^2} (\sqrt{1 + \frac{3x}{x^2}} + x}
=\lim_{x \rightarrow \infty} \frac{3x} {x (\sqrt{1 + \frac{3x}{x^2}} + 1)}
=\lim_{x \rightarrow \infty} \frac{3x} {x (\sqrt{1 + \frac{3x}{x^2}} + 1)}
=\lim_{x \rightarrow \infty} \frac{3} { (\sqrt{1 + \frac{3}{x}} + 1)}
Example 4
Evaluate \lim_{x \rightarrow \infty} (\sqrt{x^2 + x} - x).
Solution
The above function has an indeterminate form of because \lim_ {x \rightarrow \infty} (\sqrt{x^2 + x} is equal to , and \lim_ {x \rightarrow \infty} x is also equal to .
We will use the conjugate of the function 
to evaluate it. The conjugate of is 
. Multiply and divide the original function by this conjugate as shown below:
=\lim_{x \rightarrow \infty} (\sqrt{x^2 + x} - x) \cdot \frac {\sqrt{x^2 + x} + x} {\sqrt{x^2 + x} + x}
=\lim_{x \rightarrow \infty} \frac{(\sqrt{x^2 + x} - x)^2} {\sqrt{x^2 + x} + x}
=\lim_{x \rightarrow \infty} \frac{x} {\sqrt{x^2 + x} + x}
Now, we will factor out the biggest term in the denominator and write the expression like this:
=\lim_{x \rightarrow \infty} \frac{x} {\sqrt {x^2} (\sqrt{1 + \frac{x}{x^2}} + x}
=\lim_{x \rightarrow \infty} \frac{x} {x (\sqrt{1 + \frac{x}{x^2}} + 1)}
=\lim_{x \rightarrow \infty} \frac{1} { (\sqrt{1 + \frac{1}{x}} + 1)}
Did you like this article? Rate it!
Loading...
Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.