Chapters
In this article, we will discuss how to solve the exponential functions that involve limits. But before discussing this, first, let us see what is an exponential function.
What is an Exponential Function?
An exponential function is a function in which the independent variable, i.e., x is the exponent or power of the base. It is of the form:
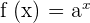
Here:
- a is a positive real number such that it is not equal to one
- The domain of the exponential function is all real numbers
- The range of the exponential function is all positive real numbers
- The y-intercept is (0, 1), and the horizontal asymptote is y is equal to zero
Standard Results of Limits
There are 5 standard results of limits which are discussed below. These standard results can be used as formulas while evaluating the limits of exponential functions.
Standard 1
\lim_{x \rightarrow a} \frac{x^n - a^n}{x - a} = n \cdot a ^ {n - 1}
Standard 2
\lim_{x \rightarrow 0} \frac{e^x - 1}{x } = 1
Standard 3
\lim_{x \rightarrow 0} \frac{a^x - 1}{x } = log_{e}a
Standard 4
\lim_{x \rightarrow 0} (1 + x) ^{\frac{1}{x}} = e
Standard 5
\lim_{x \rightarrow \infty} (1 + \frac{1}{x}) ^ x= e
In the next section, we will solve couple of examples in which we will be evaluating the limits of the exponential functions
Example 1
Evaluate the following exponential function:
\lim_{x \rightarrow 0} \frac {3 ^ {2x} - 7 ^ {4x}} {x}
Solution
It is given that the limit of the function should be evaluated as x approaches to 0. So, when we put 0 directly in the above expression, we get an indeterminate form of 
. Hence, here we will use L'Hospital's Rule which states that whenever we get an indeterminate form, we can take the derivative of the numerator and denominator separately and then apply the limit.
So, first, we will differentiate the numerator 
. The derivative of the first term is 
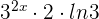. Similarly, the derivative of the second term 
is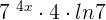 
.
Now, we will differentiate the denominator 
. The derivative of x is equal to 1. Substitute these derivatives in the above function like this:
=\lim_{x \rightarrow 0} \frac {3^{2x} \cdot 2 \cdot ln 3 - 7 ^{4x} \cdot 4 \cdot ln 7} {1}
Now, apply the limit on the above expression as shown below:
=\lim_{x \rightarrow 0} \frac {3^{0} \cdot 2 \cdot ln 3 - 7 ^{0} \cdot 4 \cdot ln 7} {1}
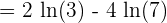
Example 2
Evaluate the following expression:
\lim_{x \rightarrow 0} \frac {5 ^ {2x} - 3 ^ {4x}} {5^{3x} - 2^{4x}}
Solution
It is given that the limit of the function should be evaluated as x approaches to 0. So, when we put 0 directly in the above expression, we get an indeterminate form of . Hence, here we will use L'Hospital's Rule which states that whenever we get an indeterminate form, we can take the derivative of the numerator and denominator separately and then apply the limit.
So, first, we will differentiate the numerator 5 ^ {2x} - 3 ^ {4x}. The derivative of the first term is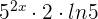 
. Similarly, the derivative of the second term 
is 
.
Now, we will differentiate the denominator 
. The derivative of the first term is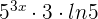 
. Similarly, the derivative of the second term 
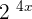is 
.
Substitute these derivatives in the above expression like this:
=\lim_{x \rightarrow 0} \frac {5^{2x} \cdot 2 \cdot ln 5 - 3 ^{4x} \cdot 4 \cdot ln 3 } {5^{3x} \cdot 3 \cdot ln 5 - 2 ^{4x} \cdot 4 \cdot ln 2}
Now, apply the limit on the above expression as shown below:
=\lim_{x \rightarrow 0} \frac {5^{0} \cdot 2 \cdot ln 5 - 3 ^{0} \cdot 4 \cdot ln 3 } {5^{0} \cdot 3 \cdot ln 5 - 2 ^{0} \cdot 4 \cdot ln 2}
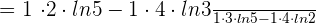
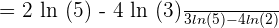
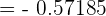
Example 3
Evaluate the limit of the following exponential function:
\lim_{x \rightarrow 0} \frac{e^x - e ^{-x}} {2x}
Solution
It is given that the limit of the function should be evaluated as x approaches to 0. So, when we put 0 directly in the above expression, we get an indeterminate form of . Hence, here we will use L'Hospital's Rule which states that whenever we get an indeterminate form, we can take the derivative of the numerator and denominator separately and then apply the limit.
First, we will find the derivative of the numerator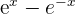 
which is equal to 
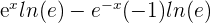. It is equal to 
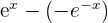. The derivative of the denominator is 2. We will substitute these values in the original function as shown below:
=\lim_{x \rightarrow 0} \frac{e^x + e^{-x}} {2}
Now, we will take the limit of the expression:
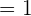
Example 4
Evaluate the limit of the following exponential function:
\lim_{x \rightarrow \infty} \frac{3^x + 2^x} {5}
Solution
It is easier to evaluate the above function because after substituting 
, we will not get the indeterminate form of or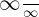 
. So, there is no need to apply L'Hospital's Rule in this example.
\lim_{x \rightarrow \infty} \frac{3^{\infty} + 2^ {\infty}} {5}
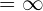
Example 5
Evaluate the following expression:
\lim_{x \rightarrow 2} \frac {5 ^ {x} + 7 ^ {3x}} {6x}
Solution
In this example, if we put x = 2 directly in the above expression, we do not get the indeterminate form, so L'Hospital's Rule is not applicable here. All we have to do is to substitute x = 2 in the above expression:
=\lim_{x \rightarrow 2} \frac {5 ^ {2} + 7 ^ {3 \cdot 2}} {6 (2)}
Example 6
Evaluate the following expression:
\lim_{x \rightarrow \infty} \frac {5e^ {4x} - e ^ {2x}} {6e^{4x} - 2^{-x} - e^ {2x}}
Solution
The primary concept that will be used in solving this problem will be the same as with the rational expressions. First, we will see the largest exponent in the numerator and the denominator, and then we will factor it out from both the numerator and the denominator. Since the limit in this example is plus infinity, hence we will only use the exponentials having positive exponents.
In this example, we will factor out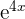 
from both the numerator and the denominator. Once we have done it, we will cancel out this common factor and take the limit of the remaining expression.
=\lim_{x \rightarrow \infty} \frac { e ^ {4x} (5 - e ^ {-2x})} {e ^ {4x} (6 - 2^{-5x} - e^ {-2x}}
Cancel out the common factor 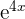from the numerator and the denominator like this:
= \lim_{x \rightarrow \infty} \frac { 5 - e ^ {-2x}} {6 - 2^{-5x} - e^ {-2x}}
Now, we will apply the limit as x approaches to infinity on the above remaining expression like this:
Did you like this article? Rate it!
Loading...
Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
∞ = -1/12
By Sriniwas aramanujan
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.