Chapters
Functions are tested with different domains to find their range. For example, you are asked to find the range of function,  . When you insert domain values, you get a definite answer. When you place the value zero, it results in infinity which is undefined. Now, you will try putting values near zero such as
. When you insert domain values, you get a definite answer. When you place the value zero, it results in infinity which is undefined. Now, you will try putting values near zero such as 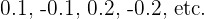 to check whether you are still getting infinity. These values do give a definite answer, it means that at zero, the function becomes undefined. In the language of limits, the function approaches infinity when you input zero in the function. The purpose of the limit is to test the value whether it gives you infinity or not.
to check whether you are still getting infinity. These values do give a definite answer, it means that at zero, the function becomes undefined. In the language of limits, the function approaches infinity when you input zero in the function. The purpose of the limit is to test the value whether it gives you infinity or not.

Limit of a Function at a Point
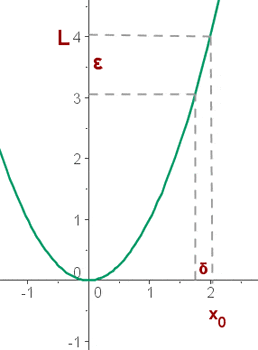
When you apply the limit to a function, it approaches that point. Normally, it approaches the point from a positive direction to that point but you can change the direction of the approaching. For example, limit is applied on function, 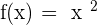 at
at  . It will approach from positive direction to
. It will approach from positive direction to  and below are the results:
and below are the results:
| x | f(x) |
|---|---|
| 1,9 | 3,61 |
| 1,99 | 3,9601 |
| 1,999 | 3,996001 |
| ... | ... |
| ↓ | ↓ |
| 2 | 4 |
As you can check the result that the output of the function is converging to  . Did you notice something? All the values approaching
. Did you notice something? All the values approaching  are in
are in  s. Let's say you want to test the continuity of the function, you need to check whether you are still getting
s. Let's say you want to test the continuity of the function, you need to check whether you are still getting  from the opposite direction? It means that the limit will be approached from the negative direction to that point. Below are the results:
from the opposite direction? It means that the limit will be approached from the negative direction to that point. Below are the results:
| x | f(x) |
|---|---|
| 2,1 | 4.41 |
| 2,01 | 4,0401 |
| 2,001 | 4,004001 |
| ... | ... |
| ↓ | ↓ |
| 2 | 4 |
Since the limit is coming from the negative direction, that means that all the value will be greater than  but they will be close to
but they will be close to  like in the above table,
like in the above table,  .
.
In nutshell, the limit of the function, f(x), at point,  , is essentially the value of y when x approaches x0. In the example, when x becomes closer to 2 from the left and right side the value of the function will approach 4.
, is essentially the value of y when x approaches x0. In the example, when x becomes closer to 2 from the left and right side the value of the function will approach 4.
It is said that the limit of the function, f(x), as x tends to x0, is L. If a real positive number is set, ε, greater than zero, there will be a positive number, δ, depending on ε, for all the values of x that differ from x0 that fulfil the condition |x - x0| < δ, and holds that |f(x) - L| <ε.
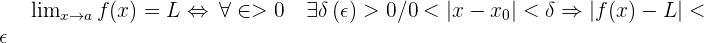
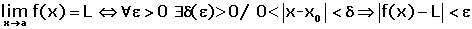













Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
∞ = -1/12
By Sriniwas aramanujan
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.