Chapters
The limit of a function at a specific point (from its domain) is the point that the function approaches. Limit is also the fundamental concept of calculus because mathematicians use derivation to analyze the behaviour of the function when it approaches that specific point. In some cases, definite integral might also be used.
Calculating the Limit at a Point
Functions are tested with limits at a specific point. It doesn't matter what kind of function is, the objective is to test whether the function approaches that specific point or not. If f(x) is a common function (polynomial, rational, radical, exponential, logarithmic, etc.) and is defined at point a, then the notation is as follows:
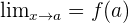
The answer to these limits shouldn't be either infinity or an imaginary number. In case if any of those answers come up, you will need to use differentials.
Examples
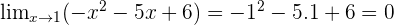
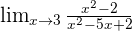
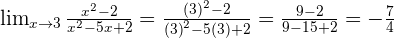
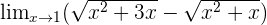
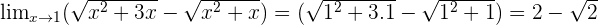
cannot be calculated because the domain is in the interval 
, therefore the values that are close to 
cannot be taken.
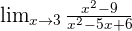
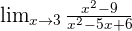is calculated and 
is not in the domain, 
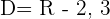, domain values as close to 3 as possible can be taken.
Calculating the Limit of a Piecewise Function
Applying limits on piecewise function is tricky. It is because of piecewise function behaves differently on different inputs. To find limits, you need to approach that point from two sides. Below are the steps to find the limit of a piecewise function:
- First, study the side limits.
- If they coincide, this is the value of the limit.
- If they do not coincide, the limit does not exist.
Example
.
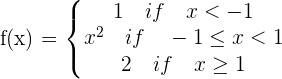At 
, the side limits are:
Left side limit: 
Right side limit: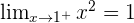 
In both cases, they coincide, therefore, the limit is 1.
At 
, the side limits are:
Left side limit: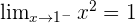 
Right side limit: 
There is no limit at .
Calculation of Limits as x ∞
Before we talk about limits that are approaching infinity, we want to discuss infinity, so what is infinity? It is a number that you can't define. The question is why do we use infinity when we can't define it? It is usually a representation that the number is unlimited without a bound. Therefore, if you see the infinity symbol that means the number is too big to be calculated. It can be either positive infinity or negative infinity. When the limit is approached infinity, that means that we are testing the function how it behaves if the input is infinity. You might be thinking that the function output will be infinity, this might surprise you that not this isn't true. Let's have a look at some examples:
Polynomial Limits
The limit as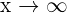 
of a polynomial function is 
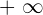or 
whether the term of the highest degree is positive or negative.
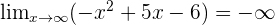
In the above example, plugging infinity in the value of x results in infinity but it is not true in every case.
If P(x) is a polynomial, then:
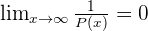
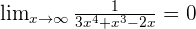
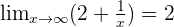
We all know that anything divided by infinity results in zero, hence any degree polynomial in denominator will give you zero if you place infinity in the values of x.
Calculation of Limits as x -∞
In the above chapter, we considered only positive infinity but what about negative infinity? Nothing much will change except the sign of the function. There are two ways to solve it. Either you place the negative infinity in the function or you change the sign of the function (with respect to their power) and then place positive infinity. Both will result in the same, let us show you how.
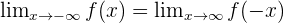
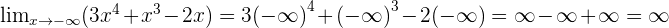
Examples
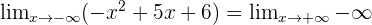
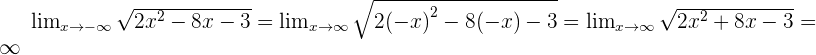
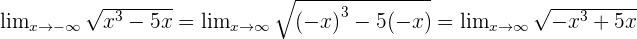
There is no limit, because the radical has negative values.
Did you like this article? Rate it!
Loading...
Correct equals infinity equals 16 but not true. It’s it’s six it’s infinity.
∞ = -1/12
By Sriniwas aramanujan
And this, my friends, is why humans will be conquered by AI… so many logic holes it’s… well, infinite. lol
Is 0^infinity ( zero to the power infinity) indeterminate form? How?
Didn’t Cantor proved that there are a group of infinities (the Aleph zero & Aleph one sets, for example)? And these are grouped around the concept of infinite to the power infinity, if I remember correctly .
Exercise 3
I think it is discontinuous at 0
exercise 2 : the function is not defined for x= 0.
exercise 1 q 5 The function has a jump discontinuity at x = 1, should be x=0.