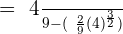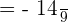Chapters
Introduction
There are situations when we can use substitution to solve a difficult piece of integration. In the substitution method, we change the variable and the integrand. When finding definite integrals, we can also change the limits of integration. To carry out integration through substitution requires practice. In this article, we will discuss what is integration by substitution method and how to use this technique to solve problems related to integration. So, let us get started.
Integration by Substitution
Integration by substitution also referred to as U-Substitution or "The reverse chain rule" is a technique to integrate a function, by setting it up in a special way. This substitution technique for finding an integral is used when an integral contains some function and its derivative. In these situations, we can substitute the function with u and rewrite the integral in terms of the new substituted variable u. This process helps in finding the integral of the function easily. The technique of integration by substitution or change of variable depends on the derivative of the composite function or chain rule.
When to Use Integration By Substitution Method
We use integration by substitution when we come across the following two types of problems:
- Integrals of the form
. In these kinds of problems, we substitute u with g(x) to simplify the integrand. - Integrals of the form
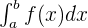, when f is a strange function, whose antiderivative is unknown. In this case, we will substitute the function x = h (u) to transform the integrand into a function whose antiderivative can be calculated easily.
Steps for Finding the Integrals Through Substitution Method
Follow the following steps to integrate the functions through substitution method:
Step 1: Select a substitution to make.
Step 2: Write dx in terms of du.
Step 3: Calculate the new integral.
Step 4: Consider the limits. (For definite integrals only)
Step 5: Substitute back again. (For indefinite integrals only)
If we are computing the indefinite integral, then we can skip step 4, as it is only for definite integral. Now, we will use the above steps to solve the following problems using integration by substitution method.
Example 1
Find the integral of the following function:
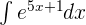
Solution
Use the following step by step approach to find the integral.
Step 1: Select a substitution to make
In this case, we will choose u = 5x + 1. Hence, the function will become:
Step 2: Write dx in terms of du
If u = 5x + 1, then 
and 
. Substitute in the above transformed function that we got after substitution:
Step 3: Calculate the new integral
Now, the substitution has been done, so we can calculate the integral of the new function. First, move the fraction 
on the left side of the integral sign:
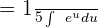
The antiderivative of 
is 
.
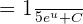
Step 4 - Substitute back again
Since, we are calculating the indefinite integral in this question, so we will substitute back again in the last step. Substitute u = 5x + 1, in the function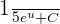 
to get the final answer:
Example 2
Find the integral of the following function:
Solution
Use the following step by step approach to find the integral.
Step 1: Select a substitution to make
In this case, we will choose u = 7x + 1. Hence, the function will become:
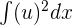
Step 2: Write dx in terms of du
If u = 7x + 1, then 
and 
. Substitute in the above transformed function, we got after substitution:
Step 3: Calculate the new integral
Now, the substitution has been done, so we can calculate the integral of the new function. First, move the fraction 
on the left side of the integral sign:
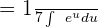
The antiderivative of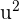 
is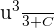 
.
Step 4 - Substitute back again
Since, we are calculating the indefinite integral in this question, so we will substitute back again in the last step. Substitute u = 7x + 1, in the function 
to get the final answer:
Example 3
Find the integral of the following function:
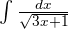
Solution
Use the following step by step approach to find the integral.
Step 1: Select a substitution to make
In this case, we will choose u = 3x + 1. Hence, the function will become:
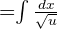
Step 2: Write dx in terms of du
If u = 3x + 1, then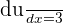 
and 
. Substitute in the above transformed function, we got after substitution:
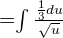
Step 3: Calculate the new integral
Now, the substitution has been done, so we can calculate the integral of the new function.
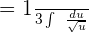
The antiderivative of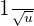 
is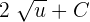 
.
Step 4 - Substitute back again
Since, we are calculating the indefinite integral in this question, so we will substitute back again in the last step. Substitute u = 3x + 1, in the function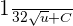 
to get the final answer:
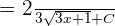
Example 4
Evaluate the following integral:
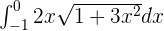
Solution
Follow the following step by step approach to integrate the above function by substitution method.
Step 1: Select a substitution to make
Suppose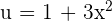 
. Substitute this value in the original function to get the following new function:
Step 2: Write dx in terms of du
If 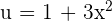, then 
. This results in 
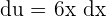and 
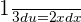Substitute 
in the above transformed function, we got after substitution:
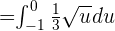
Step 3 - Calculate the Integral
To calculate the integral, move 
on the left side of the integral sign like this:
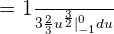
Step 4 - Consider the limits
Since we are calculating the definite integral, so we have to consider the limits here. Before considering the limits, we will substitute 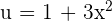again in the function we got in step 3 like this:
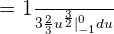
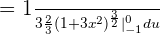
Now, we will substitute 0 and -1, using fundamental theorem of calculus like this:
Did you like this article? Rate it!
Loading...
