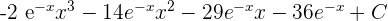Chapters
In this article, we will discuss how to integrate a function using integration by parts method, when to use this method, and its formula along with the relevant examples.

Integration by Parts
In calculus, integration by parts, also known as partial integration, is a process used to calculate the integral of the product of functions in terms of the integral of the product of derivative and antiderivative. Partial integration is often used to convert the antiderivative of the product of functions into an antiderivative for which the answer can be easily determined.
Integration By Parts Formula
The formula of partial integration or integration by parts is used to integrate the product of two functions. This technique works by calculating the integrals by reducing them into standard forms. For instance, if we have to calculate the integration of the function 2x cos x, then we can use this formula. In such cases, the integrand is the product of two functions. The formula for partial integration is given below:

We can also write the formula like this:
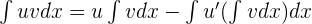
Remember the following important points while using the integration by parts method to integrate the function:
- We cannot use the integration by parts method to integrate the functions such as

- No constant is added while integrating the second function using this method
Ilate Rule
In partial integration or integration by parts, we have discussed that if the product of two functions are given, then we apply the relevant formula. The integrals of two functions are calculated, by assuming the left term as a first function and the second term as a second function. This method is known as Ilate rule.
Let suppose that you need to integrate a function 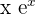 . In this case, we assume x as the first function and
. In this case, we assume x as the first function and  as the second function. It means that the first function is selected in such a manner that the derivative of the function can be integrated easily. This rule is preferred on inverse, algebraic, logarithmic, trigonometric, and exponential functions.
as the second function. It means that the first function is selected in such a manner that the derivative of the function can be integrated easily. This rule is preferred on inverse, algebraic, logarithmic, trigonometric, and exponential functions.
Now, we will solve a couple of examples using the integration by parts method.
Example 1
Evaluate the following integral:

Solution
The above function is a product of two function, hence, we can easily integrate it using integration by parts method.
The first function is 2x + 7, whereas the second function is  . We know that the formula for integral by parts is:
. We know that the formula for integral by parts is:

Suppose, 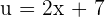 , and
, and  . We will differentiate the first function and integrate the integrate the second function as required by the formula:
. We will differentiate the first function and integrate the integrate the second function as required by the formula:
If u = 2x + 7, then 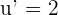
If  , then
, then 
Substitute the above values in the following integral by parts formula:
= 
= 
= 
Example 2
Evaluate the following integral:
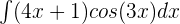
Solution
The above function is a product of two function, hence, we can easily integrate it using integration by parts method.
The first function is 4x + 1, whereas the second function is 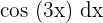 . We know that the formula for integral by parts is:
. We know that the formula for integral by parts is:

Suppose,  , and
, and  . We will differentiate the first function and integrate the integrate the second function as required by the formula:
. We will differentiate the first function and integrate the integrate the second function as required by the formula:
If u = 4x+ 1, then 
If  , then
, then 
Substitute the above values in the following integral by parts formula:
= 
= 
= 
Example 3
Evaluate the following integral:
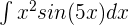
Solution
The above function is a product of two function, hence, we can easily integrate it using integration by parts method.
The first function is  , whereas the second function is
, whereas the second function is 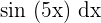 . We know that the formula for integral by parts is:
. We know that the formula for integral by parts is:

Suppose,  , and
, and 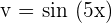 . We will differentiate the first function and integrate the integrate the second function as required by the formula:
. We will differentiate the first function and integrate the integrate the second function as required by the formula:
If  , then
, then 
If 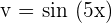 , then
, then 
Substitute the above values in the following integral by parts formula:


Example 5
Evaluate the following integral:

Solution
The above function is a product of two function, hence, we can easily integrate it using integration by parts method.
The first function is 4x - 9, whereas the second function is  . We know that the formula for integral by parts is:
. We know that the formula for integral by parts is:

Suppose, 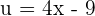 , and
, and  . We will differentiate the first function and integrate the integrate the second function as required by the formula:
. We will differentiate the first function and integrate the integrate the second function as required by the formula:
If u = 4x - 9, then 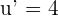
If  , then
, then 
Substitute the above values in the following integral by parts formula:
= 
= 
= 
Example 6
Evaluate the following integral:

Solution
The above function is a product of two function, hence, we can easily integrate it using integration by parts method.
The first function is 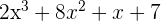 , whereas the second function is
, whereas the second function is  . We know that the formula for integral by parts is:
. We know that the formula for integral by parts is:

Suppose, 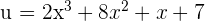 , and
, and  . We will differentiate the first function and integrate the integrate the second function as required by the formula:
. We will differentiate the first function and integrate the integrate the second function as required by the formula:
If 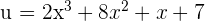 , then
, then 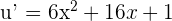
If 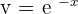 , then
, then 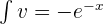
Substitute the above values in the following integral by parts formula:
=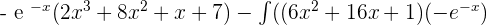
=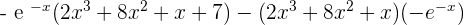
=