Chapters
Introduction
In this article, we will discuss the concept of integration, its types, and rules along with the relevant examples.
Integration refers to the process of calculating the integral. In mathematics, integrals are used to find several quantities which help us in one way or the other. These qualities include volumes, area, and displacement, etc. When we say that we are calculating the integral of a function, then we are usually referring to the definite integral of that function. For antiderivatives, we use indefinite integrals. The integral symbol is 
. In calculus, we use the concept of limit when we are dealing with the problems of algebra and geometry. Finding integrals is included in one of the major branches of calculus known as integral calculus.
How Integration Differs From Differentiation
In calculus, there are two fundamental concepts: differentiation and integration. The integration is a reverse process of differentiation. The integration refers to the summation of discrete data. It means that the process of integration is about adding or summing up the individual parts to calculate the whole. The integration method is used to calculate the summation on a vast scale. We can easily find answers to small addition problems using calculators, however, for bigger problems, we use the process of integration. In these problems, sometimes the limits reach to infinity. The purpose of finding integrals is to find functions such as volume, area, and displacement, which we are unable to find singularly due to a collection of small data. In calculus, the two major concepts, i.e. differentiation and integration of a function are associated using an important theorem known as the "Fundamental Theorem of Calculus".
Types of Integrals in Mathematics
We have already discussed the concept of integration in detail in the previous section. Now, we will see what are the two types of integrals in mathematics. There two types of integrals are:
- Definite integral
- Indefinite integral
Definite Integral
An integral that has upper and lower limits is known as a definite
integral
A definite integral is represented like this:
Indefinite Integral
The integral that does not contain upper and lower limits is known as an indefinite integral
An indefinite integral is represented like this:
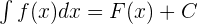
Here, C is a constant and the function f(x) is known as an integrand.
Integral Rules
Integration of a Constant:
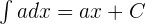
Multiplying by Constant:
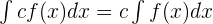
Power Rule:
Sum/ Difference Rule:
Trigonometric Integrals
Some of the important integrals of trigonometric functions are given below:
1. 
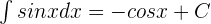
2. 
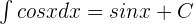
3. 
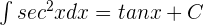
4. 
Now, in the next section, we will solve a couple of examples in which we will compute definite and indefinite integrals of the given functions.
Example 1
Find 
Solution
In the first step, we will break down the integrals using certain integration rules such as addition/subtraction or multiplication by constants. Using these rules, we can rewrite the above function like this:
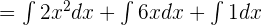
In the next step, we will shift the constants before the integral signs as shown below:
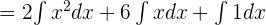
Remember the power rule of integrals 
. We will use it to calculate the integrals of the powers and integral constant rule to find the integral of the constant term of the above polynomial:
In the last step, write the final answer in its most simplified form like this:
Example 2
Calculate the integral of the following exponential function:
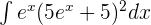
Solution
Expand the above exponential function to get the following function:
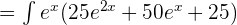
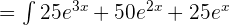
Now, we will use the integration sum rule to write the above function like this:
= 
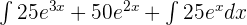
We will calculate integral of each term separately like this:
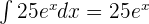
Using the above integrals, we can write the final answer like this:
= 
Example 3
Find the integral of the following exponential function:
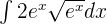
Solution
We will use the substitution method to solve this example.
Suppose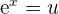 
. It means that 
and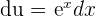 
. We will use these values in the equation below like this:
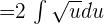
Apply the power rule 
to compute the antiderivative of the above function:
= 
= 
Substitute 
again in the above equation to get:
= 
= 
Example 4
Find the definite integral of the following function:
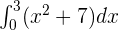
Solution
In the first step, we will find the indefinite integral, i.e. antiderivative of the function 
. The antiderivative of this function is 
. For the ease of calculation, use C = 0.
According to the fundamental theorem of calculus:
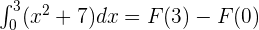
Substitute 3 and 0 in the antiderivative of the function:
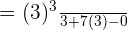
Example 5
Calculate the definite integral of the following function:
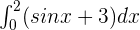
Solution
In the first step, we will find the antiderivative of the function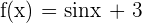 
. The antiderivative of this function is 
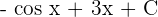. For your ease, substitute C = 0.
According to the fundamental theorem of calculus:
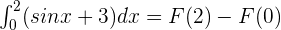
Substitute 3 and 0 in the antiderivative of the function:
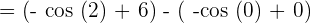
Example 6
Find the definite integral of the following function:
Solution
In the first step, we will find the indefinite integral, i.e. antiderivative of the function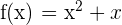 
. The antiderivative of this function is 
. For the ease of calculation, use C = 0.
According to the fundamental theorem of calculus:
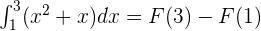
Substitute 3 and 1 in the antiderivative of the function:
= 
= 
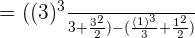
Did you like this article? Rate it!
Loading...
