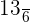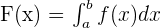Chapters

Introduction
The fundamental theorem of calculus is a theorem that associates the concept of integration of a function with the differentiation of that function. The fundamental theorem of calculus proves this association by calculating the difference between the antiderivative at upper and lower limits of the integration procedure. In this article, we will discuss the first and second parts of the fundamental theorem of calculus in detail along with the relevant examples.
Fundamental Theorem of Calculus - Part 1
The first part of the fundamental theorem of calculus is also referred to as the first fundamental theorem of calculus. It states that one of the antiderivatives, also known as indefinite integral, for instance, F, of a function f, can be computed as integral of f with a varying bound of integration. Hence, we can say that a continuous function can have antiderivatives. The proper definition of this part of the theorem is explained below:
If f is a continuous function on a closed interval, let say [a,b] and A (x) is the area of the function, then the derivative of the area of the function A'(x) is equal to f(x) for 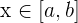 .
.
OR
Suppose f is a continuous real valued function that is defined on a closed interval [a, b], then for all of x is [a,b] can be defined by the function F in the following way:
Fundamental Theorem of Calculus - Part 2
The second part of the fundamental theorem of calculus says that, if f is the function that is continuous on a closed interval, let say, [a, b], and F represents an indefinite integral of the function "f" on the closed interval [a, b], then this part of the fundamental theorem of calculus is denoted as:

Here, the right hand side of the above equation shows the integral of f(x) with respect to x.
f(x) represents an integrand
dx shows an integrating agent
"a" shows the upper limit of the integral and "b" reflects the lower limit of the integral.
A definite integral function has a distinct value. We can express the definite integral of the function as a limit of a sum. In case there is an antiderivative F of the function in the closed interval [a, b], then the definite integral of the function represents the difference between the values of F, i.e., F(b) - F(a).
Steps to Calculate the Integral of a Function Using Fundamental Theorem of Calculus
Follow the steps below to compute the integral of the given function using the fundamental theorem of calculus:
Step 1 - Compute the antiderivative of the function
Step 2 - Use the fundamental theorem of calculus by substituting the values (upper and lower limits) in the anti-derivative of the function
Step 3 - Take the difference and simplify the answer
In the next section, we will solve a couple of examples in which we will calculate the definite integral of the function using the fundamental theorem of calculus.
Example 1
Calculate the definite integral of the following function:
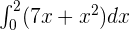
Solution
In the first step, we will find the antiderivative of the function  . The antiderivative of this function is
. The antiderivative of this function is  . Consider C = 0.
. Consider C = 0.
In the second step, we will use the fundamental theorem of calculus. According to the fundamental theorem of calculus:

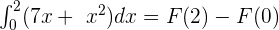
Now, we will substitute upper and lower limits which are 2 and 0 in the antiderivative of the function:
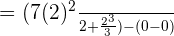
In the last step, we will take the difference and simplify the answer:
= 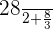
= 
Example 2
Calculate the definite integral of the following function:
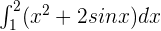
Solution
In the first step, we will find the antiderivative of the function 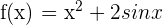 . The antiderivative of this function is
. The antiderivative of this function is 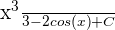 . Consider C = 0.
. Consider C = 0.
In the second step, we will use the fundamental theorem of calculus. According to the fundamental theorem of calculus:

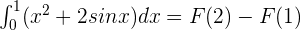
Now, we will substitute upper and lower limits which are 2 and 1 in the antiderivative of the function:
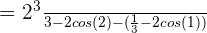
In the last step, we will take the difference and simplify the answer:
= 
= 
Example 3
Calculate the definite integral of the following function:
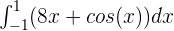
Solution
In the first step, we will find the antiderivative of the function  . The antiderivative of this function is
. The antiderivative of this function is 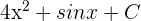 . Consider C = 0.
. Consider C = 0.
In the second step, we will use the fundamental theorem of calculus. According to the fundamental theorem of calculus:


Now, we will substitute upper and lower limits which are 2 and 0 in the antiderivative of the function:
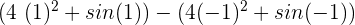
In the last step, we will take the difference and simplify the answer:
= 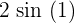
Example 4
Calculate the definite integral of the following function:

Solution
In the first step, we will find the antiderivative of the function 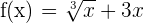 . The antiderivative of this function is
. The antiderivative of this function is 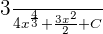 . Consider C = 0.
. Consider C = 0.
In the second step, we will use the fundamental theorem of calculus. According to the fundamental theorem of calculus:


Now, we will substitute upper and lower limits which are 2 and 0 in the antiderivative of the function:
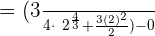
In the last step, we will take the difference and simplify the answer:
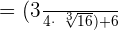
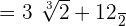
Example 5
Calculate the definite integral of the following function:
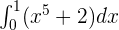
Solution
In the first step, we will find the antiderivative of the function  . The antiderivative of this function is
. The antiderivative of this function is 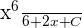 . Consider C = 0.
. Consider C = 0.
In the second step, we will use the fundamental theorem of calculus. According to the fundamental theorem of calculus:


Now, we will substitute upper and lower limits which are 1 and 0 in the antiderivative of the function:
= 
In the last step, we will take the difference and simplify the answer:
= 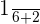
=