Chapters
- Exercise 1
- Exercise 3
- Exercise 2
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12

Exercise 1
Calculate the area of the site bounded by the curve  and the x-axis.
and the x-axis.
Exercise 3
Find the area bounded by the line x + y = 10, the x-axis, x = 2 and x = 8.
Exercise 2
Find the area of the plane region enclosed by the curve y = ln x between the point of intersection with the x-axis and x = e.
Exercise 4
Calculate the area enclosed by the curve 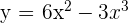 and the x-axis.
and the x-axis.
Exercise 5
Calculate the area enclosed by the curve 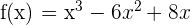 and the x-axis.
and the x-axis.
Exercise 6
Calculate the area of a circle of radius r.
Exercise 7
Find the area of an ellipse of semiaxes a and b.
Exercise 8
Calculate the area enclosed by the curve 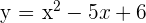 and the line y = 2x.
and the line y = 2x.
Exercise 9
Calculate the area enclosed by the parabola 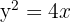 and the line y = x.
and the line y = x.
Exercise 10
Calculate the area enclosed by  and
and 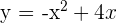 .
.
Exercise 11
Calculate the area enclosed by 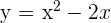 and
and 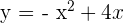 .
.
Exercise 12
Calculate the area enclosed by:
y = sin x, y = cos x, x = 0.
Solution of exercise 1
Calculate the area of the site bounded by the curve  and the x-axis.
and the x-axis.
First, find the x-intercepts to the curve and the limits of integration.
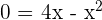


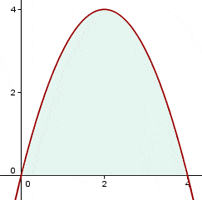

Solution of exercise 2
Find the area of the plane region enclosed by the curve y = ln x between the point of intersection with the x-axis and x = e.

First, find the x-intercepts.
ln x = 0 

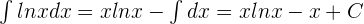
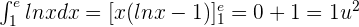
Solution of exercise 3
Find the area bounded by the line x + y = 10, the x-axis, x = 2 and x = 8.
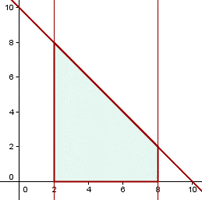

Solution of exercise 4
Calculate the area enclosed by the curve 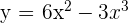 and the x-axis.
and the x-axis.
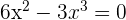
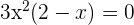


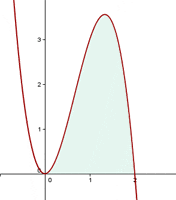

Solution of exercise 5
Calculate the area enclosed by the curve 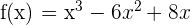 and the x-axis.
and the x-axis.
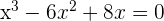
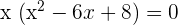




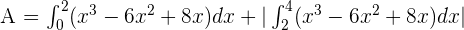
The area, for reasons of symmetry, can be written as:

Solution of exercise 6
Calculate the area of a circle of radius r.
Start from the equation of the circle  .
.
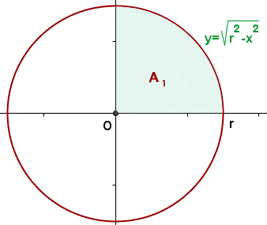
The area of the circle is four times the area of the first quadrant.
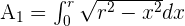
Calculate the indefinite integral by change of variable.
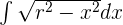
x = r sin t
dx = r cost t dt
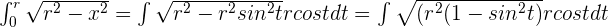

Find the new limits of integration.
x = 0 0 = r sin t sin t = 0 t = 0
x = r r = r sin t sin t = 1 

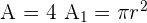
Solution of exercise 7
Find the area of an ellipse of semiaxes a and b.



As the ellipse is a symmetrical curve, the area requested will be 4 times the area enclosed in the first quadrant of the coordinate axes.

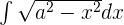
x = a sin t
dx = a cos t dt


Find the new limits of integration.
x = 0 0 = r sin t sin t = 0 t = 0
x = a a = a sin t sin t = 1 

Solution of exercise 8
Calculate the area enclosed by the curve 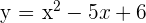 and the line y = 2x.
and the line y = 2x.
First, find the points of intersection of the two functions to know the limits of integration.
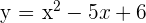 ,
, 
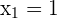
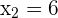
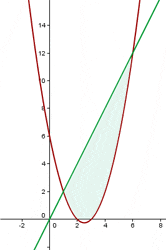
From x = 1 to x = 6, the line is above the parabola.


Solution of exercise 9
Calculate the area enclosed by the parabola 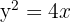 and the line y = x.
and the line y = x.
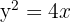 ,
, 
 (0, 0) (4,0)
(0, 0) (4,0)
From x = 0 to x = 4, the parabola is above the line.

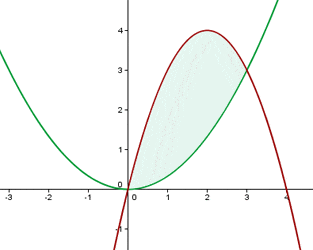
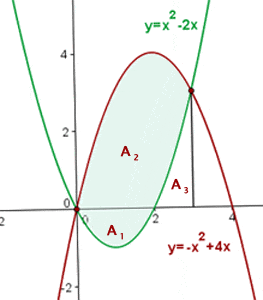
Solution of exercise 10
Calculate the area enclosed by  and
and 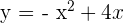 .
.
First, represent the parabolas from the vertex and the points of intersection with the axes.



V(0,0)
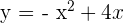

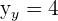
V(2, 4)



Also, find the points of intersection of the functions, which will give the limits of integration.

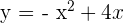
(0,0) (3,3)


Solution of exercise 11
Calculate the area enclosed by 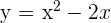 and
and 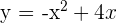 .
.
Represent the parabolas from the vertex and the points of intersection with the axes.


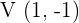
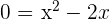

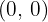
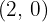

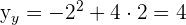
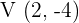
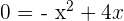
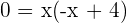

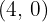
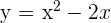 ,
, 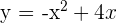
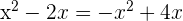
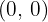




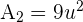


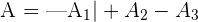

Solution of exercise 12
Calculate the area enclosed by:
y = sin x, y = cos x, x = 0.
First, find the points of intersection of the functions:
y = sin x, y = cos x
sin x = cos x

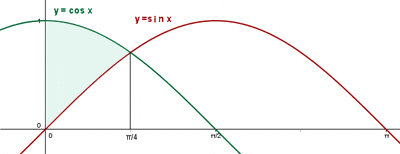
The cosine graph is above the graph within the limits of integration.














