Finding maxima and minima from a graph is easy once you understand properly. As a matter of fact, finding relative maxima and relative minima also becomes easy over time. However, not everyone has that much time to draw a graph just to calculate maxima and minima. For example, researchers don't have much time, they are looking for short cuts, one of the short cuts of finding maxima and minima is through calculus.
Calculus is a branch of mathematics and it is also one of the most frequently used as well as most complex branch. In fact, if you are an engineering student, you will know how important is calculus. Calculus is used for many purposes and one of them is to find maximum and minimum points on a graph. Using differentials might be complex but once you understand it properly, you can find maximum points in just no time.
Let's say you have a function that is differentiable at point a. Before finding the maximum points, calculus allows you to check whether the function has maximum point/points or not? The point "a" is a local extreme if:
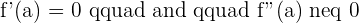
It means that when the function is differentiated, the first degree will be set equal to zero. The information you will get is the turning point of the graph. It will indicate that at this point, the graph is turning its course. This piece of information is valuable but we are not here to find the turning point, we want to find the maximum and minimum points. To get that piece of information, you need to take another derivative. The second-order derivative will determine whether the function has maximum point or minimum point or both.

Local Maxima
The method of determining maxima or minima are the same. First, you need to differentiate the function and then equate it to zero. Find the value of the variable. Then you need to derivate the function to a second degree and then place the value of the variable (that you found in the first degree) in the second-order derivative. If the value of the second-order derivative is negative, that means at that specific point, the graph has a maximum value.
STEP 1:

STEP 2:
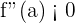
Local Minima
The same procedure will be applied. Take the first derivative and then find the value of the variable from the first derivative. Then take the second derivative and then put the value in the variable and if the value is positive that means that, at that specific point, the graph has a minimum value.
STEP 1:

STEP 2:
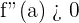
Calculation of the Maximum and Minimum
Study the maximum and minimum of the following function:
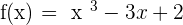
To find the local extremes, follow these steps:
1. Calculate the first derivative and its roots.
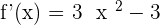

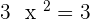


2. Calculate the 2nd derivative, and determine the sign that the zeros take from the first derivative:
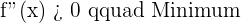

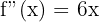


3. Calculate the image (in the function) of the relative extremes.
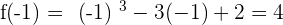
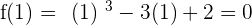
Maximum (−1, 4) Minimum (1, 0)
If the increase and decrease of a function have been studied the following can be determined:
1.
The maximum points of the function, in which it passes from increasing to decreasing.
2.
The minimum points of the function, in which it passes from decreasing to increasing.
Example
Find the maximum and minimum:
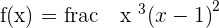
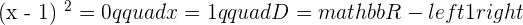
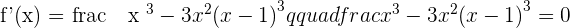

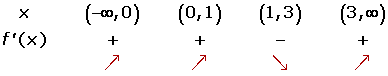
There is a minimum at  .
.
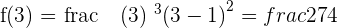
Minimum = 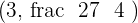
At x = 1, there is no maximum for x = 1 because it does not belong in the domain of the function.













