Chapters
Increasing and Decreasing Intervals
To understand how a function changes, we need to know the intervals over which the function changes in a particular way. A function increases over an interval when the values of a function's output increase as we increase the function's input values.
In the same way, the function decreases over an interval when the values of the function's output decrease as we decrease the input values of the function. We know that the slope depicts the average rate of change of a function at a given point. If the slope is positive, then we say that the function is increasing. The negative slope depicts a decreasing function and the zero slope shows that the function remains constant over the given interval.
Local Maximum and Local Minimum
All the functions do not increase or decrease over the entire domain. Sometimes, the function changes from increasing to decreasing for a value of the input, i.e. as the value of input increases the function value decreases. This value of input where a function's value undergoes a transition from increasing to decreasing is known as a local maximum. When we have more than one such input values, we call them local maxima.
There is another case when a function's value changes from decreasing to increasing as the input value increases. The input value, in this case, is known as the local minimum. If there are more than such input values, then we call them local minima. Both local maxima and minima are known as local extrema or local extreme values. At extrema, the function neither increases nor decreases, instead it remains constant.
Since the derivative of the function depicts the instantaneous rate of change of the function at a given point, therefore we can use it to determine the intervals of increase and decrease of a function. In the next section, we will explain this in detail.
Increasing Interval
If f is differentiable at a, then f is strictly increasing at a if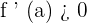 
.
Decreasing Interval
If f is differentiable at a, then f is strictly decreasing at a if 
To tell if the function is increasing or decreasing at a point, it is essential that it is differentiable. In the next section, we will solve some examples to determine the increasing and decreasing intervals using derivatives of a function.
Example 1
Study the intervals of increase and decrease of the function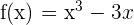 
.
Solution
We will follow the following steps to determine the intervals of increase and decrease of the above function:
Step 1 - Find the Derivative of the function
In this step, we will differentiate the function .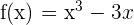
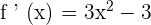
Step 2 - Obtain the roots of the first derivative of the function f ' (x)
In this step, we will obtain the roots of the first derivative of the function like this:
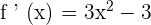
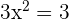
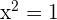
Step 3 -Test the points from all the intervals
We have got two zeroes or roots that are 1 and -1. These roots show that we have got three intervals that are 
, 
, and 
.
We will take the value from each interval and see if it is increasing or decreasing.
Lets take -2 from the interval 
and substitute it in the derivative of a function:
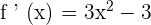
Since f ' (x) is greater than 0, so the function is increasing at this interval.
Now, let us take a point from the interval (-1, 1).
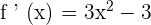
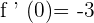
Since f ' (x) <0, therefore the function is decreasing at this interval.
Now, let us take a point from the interval and substitute it in the derivative of a function:
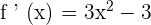
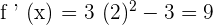
Since f ' (x) >0, hence the function is increasing at this interval.
Step 4 - Write the increasing and decreasing intervals
In step 3, we have tested the points from each interval and substituted them in the derivative of a function. We have got two intervals where the function was increasing and one interval where the function was decreasing. Hence, we can write increasing and decreasing intervals as:
Increasing: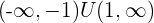 
Decreasing:
Example 2
Study the intervals of increase and decrease of the function 
.
Solution
We will follow the following steps to determine the intervals of increase and decrease of the above function:
Step 1 - Find the Derivative of the function
In this step, we will differentiate the function .
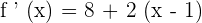
Step 2 - Obtain the roots of the first derivative of the function f ' (x)
In this step, we will obtain the roots of the first derivative of the function like this:
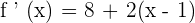
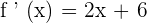
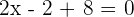
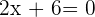
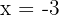
There is only one root of this derivative.
Step 3 -Test the points from all the intervals
We have got one root of the derivative of the function. We will have two intervals considering the only root of the function. These intervals are 
and 
.
We will take the value from each interval and see if it is increasing or decreasing.
Lets take -4 from the interval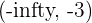 
and substitute it in the derivative of a function:
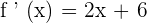
Since f ' (x) < 0, hence the function is decreasing at this interval.
Now, let us take a point from the interval
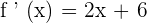
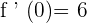
Since f ' (x) > 0, therefore the function is increasing at this interval.
Step 4 - Write the increasing and decreasing intervals
In step 3, we have tested the points from each interval and substituted them in the derivative of a function. There is only one root of the function, so we have got two intervals. We can write increasing and decreasing intervals as:
Increasing: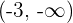 
Decreasing: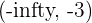
Example 3
Study the intervals of increase and decrease of the function 
.
Solution
We will follow the following steps to determine the intervals of increase and decrease of the above function:
Step 1 - Find the Derivative of the function
In this step, we will differentiate the function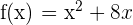 
.
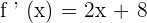
Step 2 - Obtain the roots of the first derivative of the function f ' (x)
In this step, we will obtain the roots of the first derivative of the function like this:
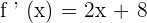
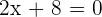
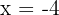
There is only one root of the derivative of this function.
Step 3 -Test the points from all the intervals
Since there is only one root, so we have got two intervals. These intervals are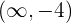 
and 
.
Let us take a point from the interval 
.
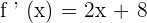
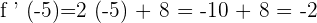
Since f ' (x) <0, therefore the function is decreasing at this interval.
Now, let us take a point from the interval and substitute it in the derivative of a function:
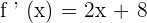
Since f ' (x) > 0, hence the function is increasing at this interval.
Step 4 - Write the increasing and decreasing intervals
In step 3, we have tested the points from each interval and substituted them in the derivative of a function. We had two intervals. In one interval the derivative of the function was less than 0, and in the other interval the derivative of the function was greater than zero. Hence, we can write the increasing and decreasing intervals as:
Increasing :
Decreasing:
Did you like this article? Rate it!
Loading...
