To understand inflection points, you need to understand what are reasons behind inflection points? For every power of a variable, there is a specific term, for example, linear equations will always have a variable that has a power of  . For quadratic equations, the power of the variable will always be
. For quadratic equations, the power of the variable will always be  , it might have a variable with a power of
, it might have a variable with a power of  as well but that isn't our main concern, if a variable has a power of
as well but that isn't our main concern, if a variable has a power of  , we will call it quadratic equation. On the other hand, if the power of the variable exceeds
, we will call it quadratic equation. On the other hand, if the power of the variable exceeds  then we will call it a polynomial equation. The word poly means "many" and the word nominal means "term". In short, polynomial means more than one term. We usually use this word, polynomial, when we are dealing with equations that have more than
then we will call it a polynomial equation. The word poly means "many" and the word nominal means "term". In short, polynomial means more than one term. We usually use this word, polynomial, when we are dealing with equations that have more than  term, however, in this lesson, we will be dealing with cubic equations only below are some examples of cubic equations:
term, however, in this lesson, we will be dealing with cubic equations only below are some examples of cubic equations:
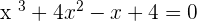
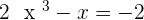
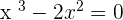
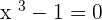
The graph of every equation is different but some of them will have a similar pattern. For example, the graph of the quadratic equation will be similar, although, the constants will affect the graph, however, you can predict the pattern of the graph. On the other hand, if you try to compare the graph of quadratic equation with a straight line equation, you can't even say they are similar, you can only say they are similar within the category (which was quadratic in the above case). The same concept is also applied to the cubic equation, there graph would be something like this:
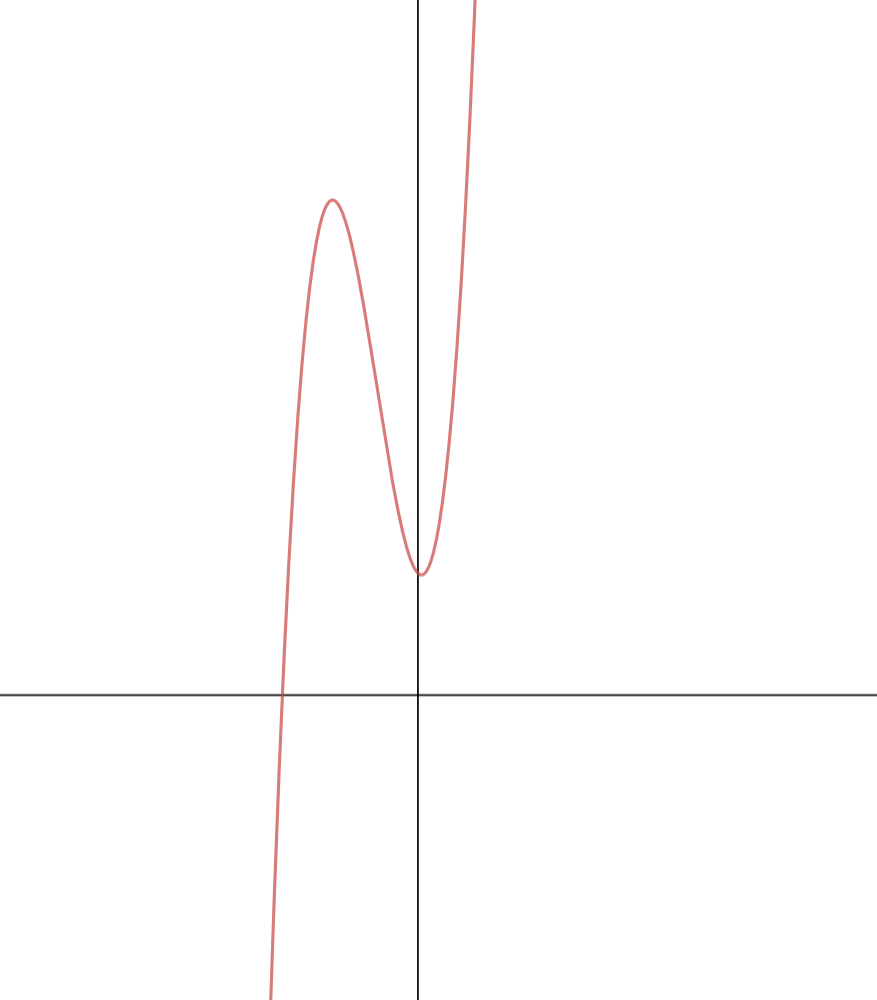
You can see two humps in this graph and that is the biggest identification of a cubic equation. That is where our point of interest comes, the inflection point. At an inflection point, the function is not concave or convex but is changing from concavity to convexity or vice versa. In simple words, a cubic equation has two parts, one is concave up and concave down. Look at the above chart once again, there are two parts of this chart. 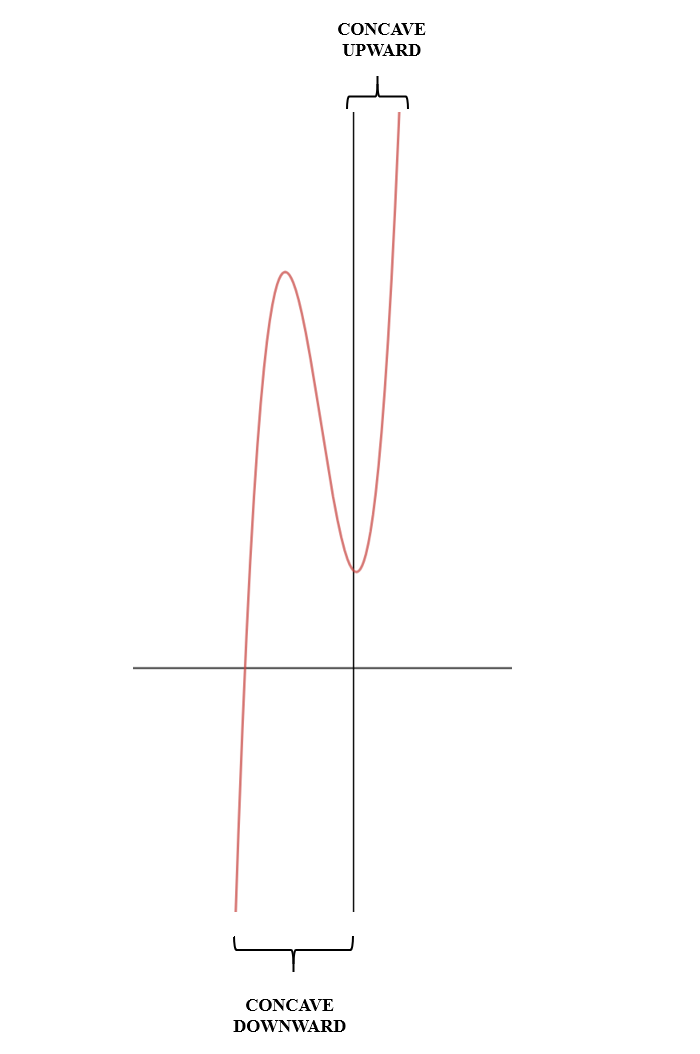
Concave upward is the point from which the slope of the graph increases and concave downward is the point from which the slope of the graph decreases. Between concave upward and concave downward, there is a point that differentiates both parts and that point is known as the inflection point. The question is, how to find the inflection point? To find that, we will use the help of calculus. When you differentiate any equation with respect to the variable in the equation, you will always get the slope. For example, differentiate 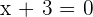 :
:
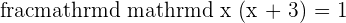
The answer  is the slope of the equation
is the slope of the equation 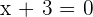 , let's prove whether it is correct or not. To prove that, we will compare the above equation with
, let's prove whether it is correct or not. To prove that, we will compare the above equation with 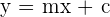 :
:
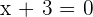
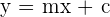
Rearranging the equation:
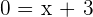
We found that 
Our point of interest is in gradient which is represented by  and the value of
and the value of  is one hence it is proved. What if we differentiate an equation two times? The result will tell us the maximum and minimum point of the equation and if you equate it to zero, the value of the variable will tell you the point of inflection.
is one hence it is proved. What if we differentiate an equation two times? The result will tell us the maximum and minimum point of the equation and if you equate it to zero, the value of the variable will tell you the point of inflection.
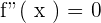 where x is the point of the inflection
where x is the point of the inflection 
One thing is clear the point of inflection exists on the cubic equation (meaning that one of the terms of the equation should have a variable that has power equal to 3).

Calculation of the Points of Inflection
Calculate the inflection points of:
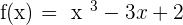
To find the inflection points, follow these steps:
1. Find the second derivative and calculate its roots.
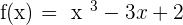
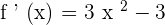
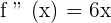
Equating  to find the inflection point.
to find the inflection point.
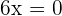

2. Determine the 3rd derivative and calculate the sign that the zeros take from the second derivative and if:
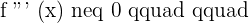 There is an inflection point
There is an inflection point
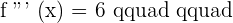 It is an inflection point.
It is an inflection point.
3. Calculate the image (in the function) of the point of inflection.
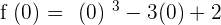

Inflection point: (0, 2)
Example
Calculate the points of inflection of the function:
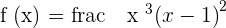
Domain:
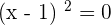
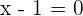
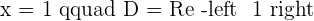
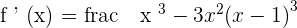
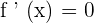




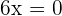

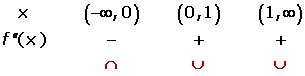
There is an inflection point at  , since the function changes from concave to convex.
, since the function changes from concave to convex.
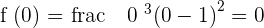
Inflection point = 













