Chapters
Quadratic Function Definition
In order to understand what a quadratic function is, let’s take a look at what a function is. A function takes a number as an input and, through a transformation on that number, results in an output. The most basic function is a linear function, structured like the following.
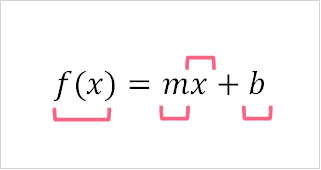
The input of a function is usually called ‘x,’ while the output of a function is typically either ‘y’ or ‘f(x).’ Take a look at some examples of linear functions below.
| x | Function | f(x) |
| 1 | f(x) = 10x + 30 | 40 |
| -4 | f(x) = -2x+1 | 9 |
| 3 | f(x) = x + 50 | 53 |
| 10 | f(x) = 2x | 20 |
While a quadratic function is still a function, it is quite different from a linear function. The definitions of both are below.
| Linear Function | Quadratic Function | |
| Standard Form | f(x) = mx + b | f(x) = a + bx + c OR f(x) = a |
| Relationship | Linear | Parabolic |
| Graph | Straight line | Parabola |
+ kQuadratic Function Properties
As you may have noticed, a quadratic function has two standard forms. The second equation is also known as the “vertex form.” You can take a look how to convert the standard form to the vertex form below.
| Step | Description | Example |
| 1 | Start with the standard form f(x) = a + bx + c | f(x) = 3 + 6x + 1 |
| 2 | For ease of notation, let f(x) be y | y = 3 + 6x + 1 |
| 3 | Move the numbers so all x’s are on one side | y -1 = 3 + 6x |
| 4 | Simplify the right side so that the term has a coefficient of 1 | y -1 = 3( + 2x) |
| 5 | We try to find the perfect square trinomial. Divide the ‘b’ term by 2, square it and that is the term we add to both sides | b term transformation:  = 1 y -1 +3(1) = 3( |
| 6 | Just note, we add 3(1) on the left side because, in reality, we’re not adding 1 on the right side but 3 * 1. | |
| 7 | Simplify the equation | y - 2 = 3 |
| 8 | Get the y term by itself again | y = 3 + 2 f(x) = 3 |
As you can see, the resulting equation is in vertex form. The reason why this is called vertex form is because the h and k terms of the equation represent the coordinates for the vertex of the parabola.
Take our example from above. The (h,k) here is (1,2). Graphing the parabola, we get:
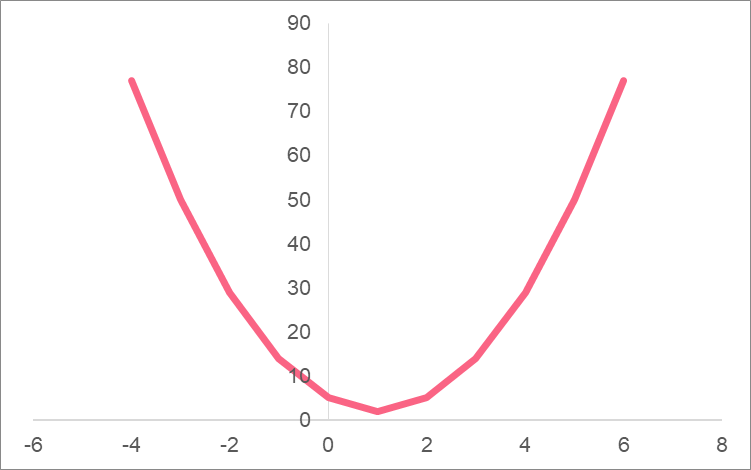
As you can see, the point where the parabola is mirrored can be found at point (1,2) on the graph. This is the definition of a vertex, where the line is defined as the axis of symmetry.
Factoring Quadratic Functions
Knowing how to factor a quadratic function can be one of the most important things that you will encounter in math relating to quadratic functions. When factoring a quadratic function, the most important rules of thumb to remember can be seen below.
| 1 | Check for a common factor |  =  |
| 2 | Find the two numbers where that equal to a*c and add up to b |  - (4 * -1) = -4 = a*c - (4 + -1) = 3 = b |
These two rules can help us get to the desired output. It’s also important to keep in mind that there is sometimes what is called a perfect square. Take a look at the form below, which gives us the following:
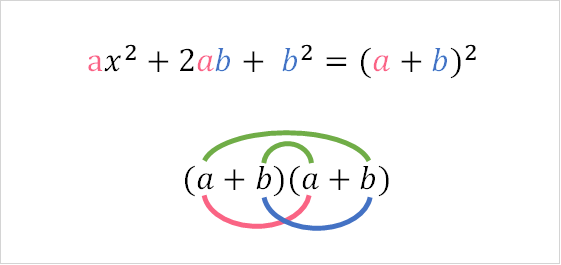
Take a look at an example of a perfect square below.
\[
(x+3)^{2} = (x+3)(x+3)
\]
\[
(x+3)(x+3) = x^{2} + 3^{2} + 3x + 3x
\]
\[
a^{2} +2ab + b^{2} = x^{2} + 6x + 3^{2}
\]
Vertex of Quadratic Function
When we talk about the vertex of a quadratic function, it is important to understand what we’re talking about. Imagine a parabola folded in half. The point where we fold it in half is called the axis of symmetry. This is because both sides of the fold contain a symmetrical part of the parabola.
The vertex of a quadratic function is the point on the graph of that function where, if we were to fold it, would correspond to the lowest or highest point. Take a look at the image below to get a better idea of the vertex.
In terms of what the point actually means, each coordinate corresponds to a different part of the function. Take a look at the table below for a description.
| h | Horizontal shift | This point determines how many spaces to the right or left the graph has shifted from 0 |
| k | Vertical shift | This point determines how many spaces up or down the graph has shifted from 0 |
Take a look at the image below to see the difference these coordinates make in the graph.
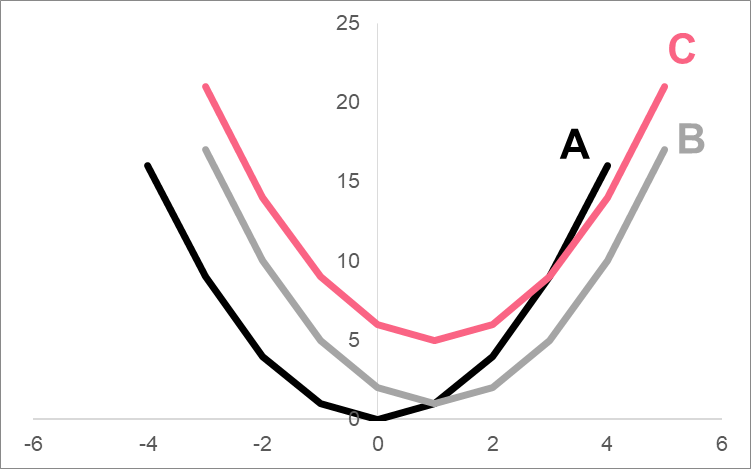
| A | B | C |
|  |  |
| (0,0) | (1,1) | (1,5) |
Problem 1
You want to know the roots to a quadratic function. Given the following function, factor the quadratic function. After factoring the function, find the roots of the function.
\[
3x^{2} + 9x - 12
\]
Problem 2
Transform the following function from the standard form to the vertex form.
\[
x^{2} + 3x - 4
\]
Problem 3
Describe the transformation that occurs from going to function A to function B. Give the vertex of both functions.
- A:
- B:
Solution Problem 1
Here is the solution to this problem:
\[
3x^{2} + 9x - 12
\]
\[
3(x^{2} + 3x - 4)
\]
\[
3(x+4)(x-1)
\]
\[
3(x+4)(x-1) = 0
\]
\[
(x+4) = 0 \; and \; (x-1) = 0
\]
The roots are -4 and 1.
Solution Problem 2
Here is the solution:
\[
y = x^{2} + 4x - 4
\]
\[
y + 4 = x^{2} + 4x
\]
\[
y + 4 + (\frac{4}{2})^{2} = x^{2} + 4x + (\frac{4}{2})^{2}
\]
\[
y + 4 + 4 = x^{2} + 4x + 4
\]
\[
y + 8 = (x+2)^{2}
\]
\[
y = (x+2)^{2} - 8
\]
Solution Problem 3
Going from to means going from vertex (1,1) to vertex (1,5). This means that while the shape of the parabola stays the same, we are shifting 5 units up for each point.
Did you like this article? Rate it!
Loading...
