Chapters
Exercise 1
Three pounds of squid can be purchased at the market for 
dollars. Determine the equation and represent the function that defines the cost of squid based on weight.
Exercise 2
It has been observed that a particular plant's growth is directly proportional to time. It measured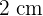 
when it arrived at the nursery and 
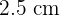exactly one week later. If the plant continues to grow at this rate, determine the function that represents the plant's growth and graph it.
Exercise 3
A car rental charge is 
dollars per day plus 
dollars per mile travelled. Determine the equation of the line that represents the daily cost by the number of miles travelled and graph it. If a total of 
miles was travelled in one day, how much is the rental company going to receive as a payment?
Exercise 4
When digging into the earth, the temperature rises according to the following linear equation:
.
t is the increase in temperature in degrees and h is the depth in meters. Calculate:
1. What the temperature will be at 
depth?
2.Based on this equation, at what depth would there be a temperature of 
?
Exercise 5
The pollution level in the centre of a city at 
is 
(parts per million) and it grows in a linear fashion by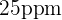 
(parts per million) every hour. If 
is pollution and t is the time elapsed after , determine:
1.The equation that relates y with t.
2. The pollution level at 4 o'clock in the afternoon.
Exercise 6
A faucet dripping at a constant rate fills a test tube with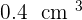 
of water every minute. Form a table of values for time and capacity, determine the equation and represent it graphically.
Exercise 7
For the function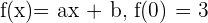 
and 
.
1. Determine the coefficients that satisfy the equation:
2. Write the equation and represent it graphically:
3. Indicate the intervals where the function has a positive and negative value.
Solution of exercise 1
Three pounds of squid can be purchased at the market for dollars. Determine the equation and represent the function that defines the cost of squid based on weight.
Since it is a directly proportional question hence, 
:
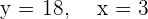
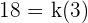
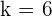
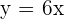
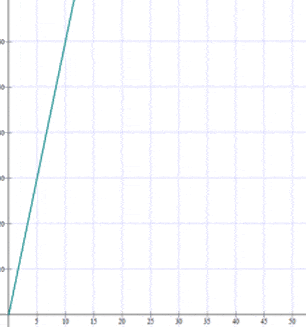
Solution of exercise 2
It has been observed that a particular plant's growth is directly proportional to time. It measured 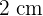when it arrived at the nursery and 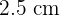exactly one week later. If the plant continues to grow at this rate, determine the function that represents the plant's growth and graph it.
Initial height =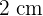
Weekly growth =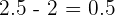 
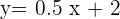
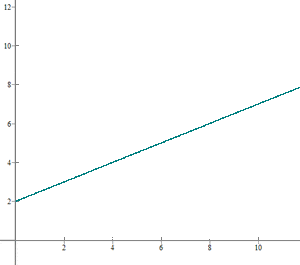
Solution of exercise 3
A car rental charge is dollars per day plus dollars per mile travelled. Determine the equation of the line that represents the daily cost by the number of miles travelled and graph it. If a total of miles was travelled in one day, how much is the rental company going to receive as a payment?
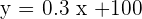
dollars
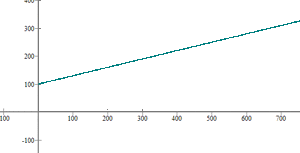
Solution of exercise 4
When digging into the earth, the temperature rises according to the following linear equation:
.
t is the increase in temperature in degrees and h is the depth in meters. Calculate:
1. What the temperature will be at depth?
2.Based on this equation, at what depth would there be a temperature of ?
Solution of exercise 5
The pollution level in the centre of a city at is (parts per million) and it grows in a linear fashion by 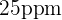(parts per million) every hour. If is pollution and t is the time elapsed after , determine:
1.The equation that relates y with t.
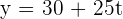
2. The pollution level at 4 o'clock in the afternoon.
10 hours have elapsed between 6 in the morning to four in the afternoon.
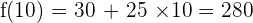
Solution of exercise 6
A faucet dripping at a constant rate fills a test tube with 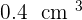of water every minute. Form a table of values for time and capacity, determine the equation and represent it graphically.
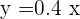
| Time | Capacity |
|---|---|
 |  |
 |  |
 |  |
|  |
| ... | ... |
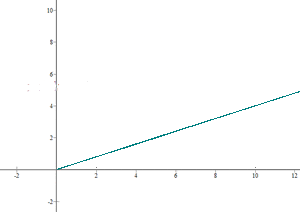
Solution of exercise 7
For the function 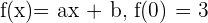and .
1. Determine the coefficients that satisfy the equation:
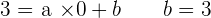
2. Write the equation and represent it graphically:
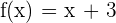
3. Indicate the intervals where the function has a positive and negative value.
Did you like this article? Rate it!
Loading...
