One of the building blocks of calculus is finding derivatives. In fact, we have a separate name for it and it is called as differential calculus. Differential calculus is the branch of calculus that deals with finding the rate of change of the function at a given point. The other significant subdivision of calculus is integral calculus which is related to the differential calculus in a way that the process of finding the derivatives and integrals are reverse of each other. The process of finding derivatives is known as differentiation and the process of finding integrals is known as integration. But in this article, we will only discuss the derivatives and how to interpret them geometrically.
Before proceeding, you must know that to understand the geometrical representation of derivatives, you should be familiar with how to differentiate the function, differential rules and finding derivatives using the limit formula. The reason behind it is that the geometric representation of the derivatives is a higher level concept and to ace it, your fundamental concepts related to differentiation must be cleared.
Derivatives
Derivative means the rate of change in one variable with respect to another variable. In other words, we can say that a derivative of the function is an instantaneous rate of change of the function at a given point. The derivatives are mathematically represented as follows:
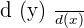
Alternatively, we also use the following notation to represent derivatives of a function:
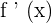
We can take as many derivatives of differentiable functions as possible. When we take the derivative of the original function, it is known as the first derivative. Similarly, when we further differentiate the first derivative, we get a second derivative and so on. We call second, third and fourth derivatives of the function higher order derivatives. We know that differentiation takes the original function as an input and then returns a derivative as an output.
We know that the graphs are used in mathematics to interpret the patterns or relationships between two variables. The graph of a function changes after differentiating a function. When we differentiate the first derivative further to find the second derivative, the graph changes again.
Geometric Interpretation
Well, it may seem a complex concept initially, but once you understand the process in detail, you will find it much easier to explain the derivatives geometrically. So, we will start with the following figure which represents a derivative of the function graphically. We have explained how to interpret or create this graph in detail below the figure.
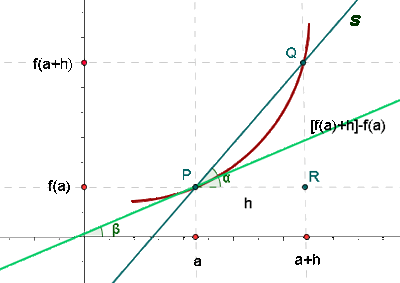
- Suppose a function
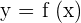is represented by a curve as shown in the above graph. - Now, the next step is to choose two points on the curve, let say they are P and Q.
- We have joined the points P and Q by a straight line. This line is called the secant line and is drawn in blue color in the above graph.
- Join the point P and Q by a straight horizontal and vertical lines to both x and y - axis. The point P joins the x - axis and we have named it as a. The point at which the point P joins the y-axis is called as f (a).
- We repeat the process for point Q and name the points where it joins the x - axis and y - axis as (a + h) and f (a + h) respectively.
- Draw a horizontal line from point P so that it touches the vertical line from point Q to x - axis at point R. The distance between the point P and R is known as h. Hence, in other words, we can say that h is equal to PR.
- Now, we can determine the coordinates of the points P and Q.
- The coordinate of the point P are (a, f (a)) and the coordinates of the point Q are (a + h , f(a + h)).
- We know that the formula for finding a derivative of the function is
\lim_ {h \rightarrow 0} \frac {f (a + h) - f (a)} {h}. - Now, you can determine the f (a + h) from the graph which is a vertical line from point Q touching the x - axis.
- Similarly, f(a) is a straight vertical line from point R to the x - axis. The difference between f (a + h) and f (a) is also represented in the graph below.
- Now, if you notice we have got a triangle PQR. If you look at this triangle carefully, you will get to know that f (a + h) - f (a) is QR and h is equal to PR. Thus you can substitute these values in the limit formula like this:
\lim_ {h \rightarrow 0} \frac {QR} {PR}
- Since, PQR is a right angle triangle, therefore you can interpret the above ratio as a trigonometric function. We know that
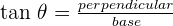. - In the above ratio, QR is perpendicular and PR is the base. Hence, this ratio is equal to
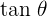. We can write it mathematically as:
\lim _ {h \rightarrow 0} tan \theta
- You can see that the we have a chord PQ which tends to be tangent at point P. Hence, we have drawn a tangent line passing through the point P. This tangent line is represented in green color in the above graph.
- Hence, we can say that the derivative of the function is the slope of this tangent line.
So, this was all about the geometric interpretation of the derivatives.
Conclusion
If we are asked to conclude the above complicated procedure of geometric interpretation of a derivative function, then we can say that the tangent line is actually the geometrical or graphical representation of the derivative. We know that different functions have different derivatives. Hence, the interpretation of these derivatives on the graph will be different and according to the situation or context. But regardless of the function type and its derivative, one thing is common in all the derivatives and that is they take the form of a tangent line to the function graph or we can say that derivatives are equal to the slope of the tangent line.
Did you like this article? Rate it!
Loading...
Like the explanation, want to rearn more. Really enjoying the documents received.