Chapters
Exercise 1
The equation of a rectilinear movement is: d(t) = t³ − 27t. At what moment is the velocity zero? Also, what is the acceleration at this moment?
Exercise 2
What is the speed that a vehicle is travelling according to the equation d(t) = 2 − 3t² at the fifth second of its journey? In this intance, space is measured in meters and time in seconds.
Exercise 3
Due to bad environmental conditions, a colony of a million bacteria does not reproduce during the first two months of a study. The function that represents the population of the colony during the entire study (time is represented in months) is given by:
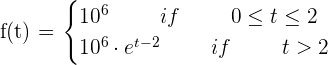
1. Verify that the population is a continuous function of time.
2. Calculate the average rate of change of the population during the interval [0, 2] and [0, 4].
3. Calculate the instantaneous rate of change at t = 4.
Exercise 4
The growth of a bacterial population is represented by the function p(t) = 5,000 + 1,000t², where t is the time measured in hours. Determine:
1. The average growth rate.
2. The instantaneous rate of growth.
3. The instantaneous growth rate at t0 = 10 hours.
Exercise 5
The equation of a circular motion is: φ(t) = ½t². What is the angular velocity and the acceleration at the seven second mark?
Exercise 6
A man is 2000 m from the base of a tower and is launching a rocket in the direction of the same tower. When the rocket takes off the change in the angle between the flight path and the land is represented by Φ(t) according to time. Knowing that Φ'(t) = Π/3, determine:
1. The height of the rocket when Φ = Π/3 radians.
2. The velocity of the rocket when Φ = Π / 3 radians?
Exercise 7
Gas is pumped into a spherical tank at 6 m³/min. If the pressure remains constant, at what velocity does the size of the radius change when the diameter is 120 cm?
Solution of exercise 1
The equation of a rectilinear movement is: d(t) = t³ − 27t. At what moment is the velocity zero? Also, what is the acceleration at this moment?
v(t) = d′t) = 3t² − 27 3t² − 27 = 0t = ± 3
a(t) = d′'(t) = 6ta(−3) = −18a(3) = 18
Solution of exercise 2
What is the speed that a vehicle is travelling according to the equation d(t) = 2 − 3t² at the fifth second of its journey? In this intance, space is measured in meters and time in seconds.
v_{5}^{t} = \lim_{h\rightarrow 0} \frac{2 - 3(5 + h)^2 - 2 + 3 \cdot 5^2}{h}
= \lim_{h \rightarrow 0} \frac{-30h - 3h^2}{h}
= \lim_{h \rightarrow 0} \frac{h (-30 - 3h)}{h}
Solution of exercise 3
Due to bad environmental conditions, a colony of a million bacteria does not reproduce during the first two months of a study. The function that represents the population of the colony during the entire study (time is represented in months) is given by:
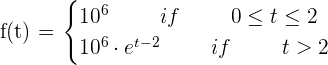
1. Verify that the population is a continuous function of time.
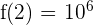
\lim_{t \rightarrow 2^ {-}} 10^6 = 10^6
\lim_{t\rightarrow 2^ {+}} 10^6 \cdot e^ {t - 2} = 10^6
2. Calculate the average rate of change of the population during the interval [0, 2] and [0, 4].
3. Calculate the instantaneous rate of change at t = 4.
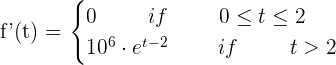
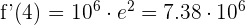
Solution of exercise 4
The growth of a bacterial population is represented by the function p(t) = 5,000 + 1,000t², where t is the time measured in hours. Determine:
1. The average growth rate.
2. The instantaneous rate of growth.
p'(x) = \lim_{g \rightarrow 0}\frac{5000+ 100(t + h)^2 - 5000 - 100t^2}{h}
= \lim_{h \rightaroow 0} (200 t - 100h) = 200 t
3. The instantaneous growth rate at t0 = 10 hours.
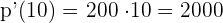
Solution of exercise 5
The equation of a circular motion is: φ(t) = ½t². What is the angular velocity and the acceleration at the seven second mark?
ω(t)= φ′(t)= t ω = 7
α(t)= φ′′ (t)= 1 α = 1
Solution of exercise 6
A man is 2,000 m from the base of a tower and is launching a rocket in the direction of the same tower. When the rocket takes off the change in the angle between the flight path and the land is represented by Φ(t) according to time. Knowing that Φ'(t) = Π/3, determine:
1. The height of the rocket when Φ = Π/3 radians.
2. The velocity of the rocket when Φ = Π/3 radians?
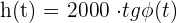
Solution of exercise 7
Gas is pumped into a spherical tank at 6 m³/min. If the pressure remains constant, at what velocity does the size of the radius change when the diameter is 120 cm?
Did you like this article? Rate it!
Loading...
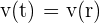
Like the explanation, want to rearn more. Really enjoying the documents received.