Chapters
Calculate the Derivatives at the Points Indicated:
Exercise 1
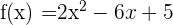at 
Exercise 2
at 
Exercise 3
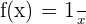at x = 2
Exercise 4
at x = 3
Exercise 5
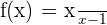at x = 2.
Exercise 6
Given the equation f(x) = 2x² − 3x − 1, find the coordinates of the point on the curve in which the tangent forms a 45° angle with the x-axis.
Solution of exercise 1
Find the value of the derivative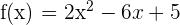 
at x = -5.
f'(x) = \lim_ {h \rightarrow 0} \frac{2 (x + h)^2 - 6 (x + h) + 5 - (2x^2 - 6x + 5)}{h}
= \lim_ {h \rightarrow 0} \frac{2x^2 + 4xh + 2h^2 - 6x - 6h + 5 - 2x^2 + 6x - 5}{h}
= \lim_ {h \rightarrow 0} \frac{4xh - 6h + 2h^2}{h} = \lim_{h\rightarrow 0} \frac{h(4x - 6 + 2h)}{h} = 4x - 6
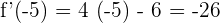
Solution of exercise 2
Find the value of the derivative at x = 1.
f' (x) = \lim_ {h \rightarrow 0} \frac{ (x + h)^3 + 2(x + h) - 5 - (x^3 + 2x - 5)} {h}
=\lim_{h \rightarrow 0} \frac{x^3 + 3x^2h + 3xh^2 + h^3 + 2x + 2h - 5 - x^3 - 2x + 5}{h}
=\lim_{h \rightarrow 0} \frac{3x^2h + 3xh^2 + h^3 + 2h}{h}
= \lim_{h \rightarrow 0} \frac{h(3x^2 + 3xh + h^2 + 2)}{h} = 3x^2 + 2
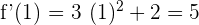
Solution of exercise 3
Find the value of the derivative 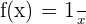at x = 2.
f'(x) = \lim_{h \rightarrow 0} \frac{\frac{1}{x + h} - \frac{1}{x}} {h}
= \lim_{h \rightarrow 0} \frac{\frac{x - (x + h)}{x (x + h)}} {h}
= \lim_ {h \rightarrow 0} \frac{\frac{-h}{x^2 + xh}} {h}
= \lim_{h \rightarrow 0} (-\frac{1}{x^2 + xh}) = - \frac{1}{x^2}
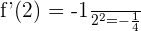
Solution of exercise 4
Find the value of the derivative at x = 3.
f'(3) = \lim_{h \rightarrow 0} \frac{\sqrt{3 + h} - \sqrt{3}} {h}
= \lim_{h \rightarrow 0} \frac{(\sqrt{3 + h }- \sqrt{3}) (\sqrt{3 + h} + \sqrt{3})} {h ( \sqrt{3 + h} + \sqrt{3})}
= \lim_{h \rightarrow 0} \frac{(3 + h) - 3} {\sqrt{3 + h} + \sqrt{3}}
= \lim_{h \rightarrow 0} \frac{h}{h(\sqrt{3 + h} + \sqrt{3})}
= \lim_{h \rightarrow 0} \frac{1}{\sqrt{3 + h} + \sqrt{3}} = \frac{1}{\sqrt{3} + \sqrt{3}} = \frac{1}{2 \sqrt{3}}
Solution of exercise 5
Find the value of the derivative 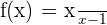at x = 2.
f'(x) = \lim_{h \rightarrow 0} \frac{\frac{x + h} {x + h - 1} - \frac{x}{x - 1}} {h}
= \lim_{h \rightarrow 0} \frac{\frac{x^2 - x + hx - h - x^2 - hx + x}{(x + h - 1) (x - 1)}} {h}
= \lim_ {h \rightarrow 0} \frac{\frac{-h}{(x + h - 1) (x - 1)}} {h} = \lim_{h \rightarrow 0} \frac{-1}{(x + h - 1) (x - 1)} = -\frac{1}{(x - 1)^2}
Solution of exercise 6
Given the equation f(x) = 2x² − 3x − 1, find the coordinates of the point on the curve in which the tangent forms a 45° angle with the x-axis .
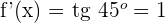
1 = \lim_{h \rightarrow 0} \frac{2 (x + h)^2 - 3(x + h) - 1 - (2x^2 - 3x - 1)} {h}
1 = \lim_{h \rightarrow 0} \frac{2x^2 + 4xh + 2h^2 - 3x - 3h - 1- 2x^2 + 3x + 1} {h}
1 = \lim_{h \rightarrow 0} \frac{h(4x + 2h - 3)}{h}
Did you like this article? Rate it!
Loading...
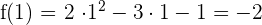
Like the explanation, want to rearn more. Really enjoying the documents received.