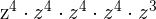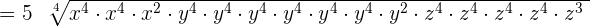Chapters
In this article, we will learn what are radicals and how to simplify the complex radical expressions. So, let us get started
What are Radicals?
Radicals are also known as roots and they are the inverse of applying exponents to the numbers or coefficients. A more formal definition of a radical expression is given below:
An expression denoted as
, in which
and
; so that when b is negative, m must be odd is known as a radical expression.
We can remove a radical by applying power and we can remove power by applying a radical. For example, the cube of 10 is 1000, and cube root of 1000 is 10. Similarly, the square of 7 is 49 and the square root of 49 is 7. Mathematically, we can express these examples as:
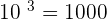
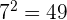
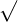is used to express a radical. We can read the expressions 
as square root 81, root 81, or simple radical 81. We can take any power other than 2 and 3 and raise the numbers to those powers. Similarly, we can take any root of a number other than 2 and 3, for instance, fourth root, fifth root, sixth root, and so on.
6 is the index of the base 5. The number inside the radical symbol is known as radicand. For example, in the expression 
, 100 is known as radicand.
Powers and Radicals
We can convert radical to power. Consider the following examples:
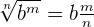
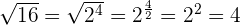
Arithmetic Operations on Radicals
We can add, subtract, multiply and divide the radical expression like we apply these operations on numbers and exponents. To add or subtract the radicals, it is essential that the numbers inside the radical symbol, i.e. radicand and the index should be the same. Multiply the radicands together to multiply the radicals. To solve the radical fractions, all we need to do is to multiply and divide the expression with the root in the denominator. This process of solving the radical fractions is known as rationalization.
Simplifying Radical Expressions
The radicals can be simplified if:
- We can convert the radicand which is the term inside the radical symbol into an exponent
- The term inside the radical symbol is a fraction
- The fraction's denominator contains a radical sign
Now, we will solve some examples in which we will simplify the radical expressions.
Example 1
Simplify
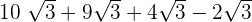
Solution
To simplify the above expression, we will first see whether the terms inside the radical symbol, i.e. radicands are same or not. In all the four terms, the radicands are same. Hence, we will simply add and subtract the terms like number and keep the radicand same like this:
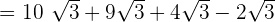
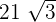
Example 2
Simplify the following radical expression:
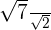
Solution
In the above expression, the radical sign is present in the denominator. Hence, we will use rationalization to simplify the above expression. In the first step, we will multiply and divide the whole expression by the term in the denominator as shown below:
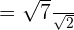
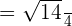
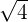is equal to 2:
Example 3
Evaluate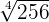 
.
Solution
256 is equal to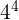 
. We can write the above expression as:
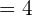
Example 4
Evaluate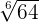 
.
Solution
64 is equal to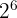 
. We can write the above expression as:
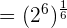
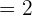
Example 5
Evaluate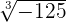 
.
Solution
-125 is equal to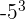 
. We can write the above expression as:
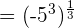
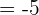
Example 6
Simplify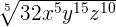 
.
Solution
We can write the above expression as an exponential expression like this:
= 
We will apply the index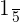 
to each term separately like this:
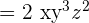
Example 7
Simplify 
.
Solution
We can write the above expression as an exponential expression like this:
= 
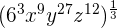
We will apply the index 
to each term separately like this:
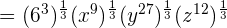
Example 8
Simplify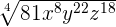 
.
Solution
We can write the above expression as an exponential expression like this:
= 
We will apply the index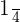 
to each term separately like this:
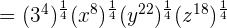
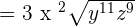
This expression can be simplified further because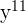 
is equal to 
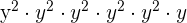and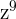 
is equal to 
.
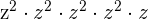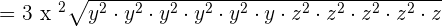
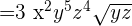
Example 9
Simplify 
.
Solution
We can write the above expression as an exponential expression like this:
= 
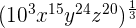
We will apply the index to each term separately like this:
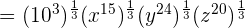
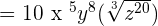
This expression can be simplified further because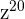 
is equal to 
.
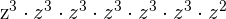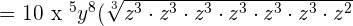
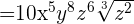
Example 10
Simplify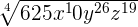 
.
Solution
We can write the above expression as an exponential expression like this:
= 
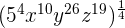
We will apply the index 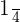to each term separately like this:
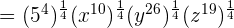
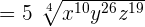
This expression can be simplified further because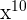 
is equal to 
, 
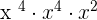is equal to 
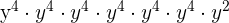and 
is equal to 
Did you like this article? Rate it!
Loading...
