Chapters

Real Number Definition
If you’re interested in operations involving real numbers, it is important to understand what a real number is. Real numbers are defined as all numbers that are:
- Whole numbers and Integers
- Rational numbers
- Irrational numbers
Take a look at some of the definitions below.
| Whole Number | Integer | |
| Definition | Positive number that doesn’t have a decimal or fraction | Positive or negative whole numbers |
| Example | 0, 2, 30, 160 | -4, -90, 0, 3, 88 |
Now that you know the difference between whole numbers and integers, let’s compare rational and irrational numbers.
| Rational | Irrational | |
| Definition | Positive or negative number that has a decimal or fraction | Positive or negative numbers that can’t be written as a decimal or fraction |
| Example | 0.55, -0.88,  |  , ,  , , 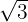 |
Basic Maths Operations
Basic math operations involve the following:
- Addition
- Subtraction
- Multiplication
- Division
Addition is when two numbers are combined as a new sum.


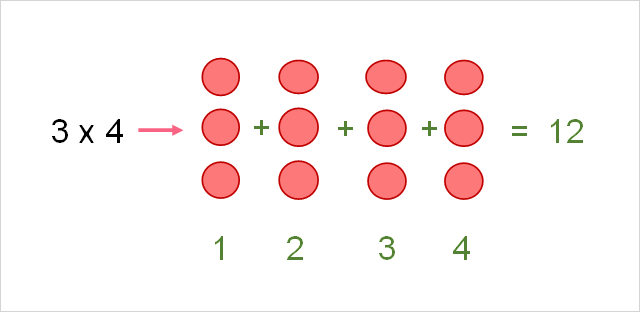
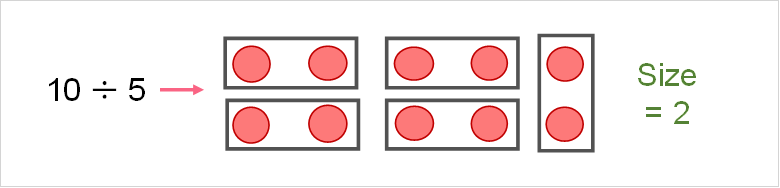
Operations with Positive and Negative Numbers
There are a couple of rules you should remember with respect to signs. Signs tell us whether a number is positive (+) or negative (-).
When you perform addition or subtraction, signs can change depending on the absolute value of the numbers. Take for example two scenarios:

| Rule | Example | Absolute Value |
| A | 10 + (-5) = 5 | 10 > |-5| -> 10 > 5 |
| B | 10 + (-11) = -1 | 10 < |-11| -> 10 < 11 |
Multiplication and division rules are much easier.

| Rule | Example |
| A | 4 x 4 = 16 |
| B | 3 x -2 = -6 |
| C | 4 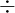 2 = 2 2 = 2 |
| D | 15 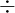 -3 = -5 -3 = -5 |
Order of Operations
When we have a combination of operations in a single expression, it can be confusing to understand what operation we should do first. This is where the acronym PEMDAS comes in handy.
| Description | Symbol | |
| P | Parenthesis | () |
| E | Exponent |  |
| M | Multiplication | x |
| D | Division | 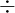 |
| A | Addition | + |
| S | Subtraction | - |
In order to solve this, let’s take a look at an example:
\[
(5 + 3) \div 2 * 2 - 3 + 1
\]
The steps are below.
| Step | Operation | Why | Remaining |
| 1 | (5 + 3) = 8 | P |  |
| 2 | 2 * 2 = 4 | M |  |
| 3 | 8 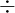 4 = 2 4 = 2 | D | 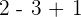 |
| 4 | 3 + 1 = 4 | A |  |
| 5 | 2 - 4 = -2 | S |
Commutative Law
The commutative law states that order does not matter in an operation. Note that this only applies to addition and multiplication.
Addition
In addition, the order in which you add each number does not matter. This can be written as the following:
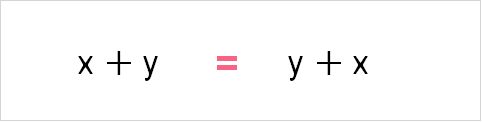
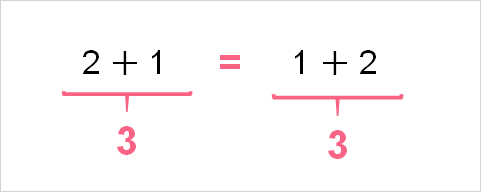
Multiplication
In multiplication, the order in which you multiply each number does not matter. This can be written as the following:
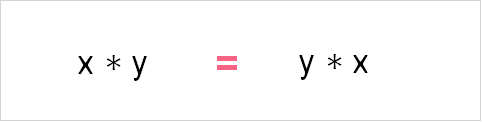
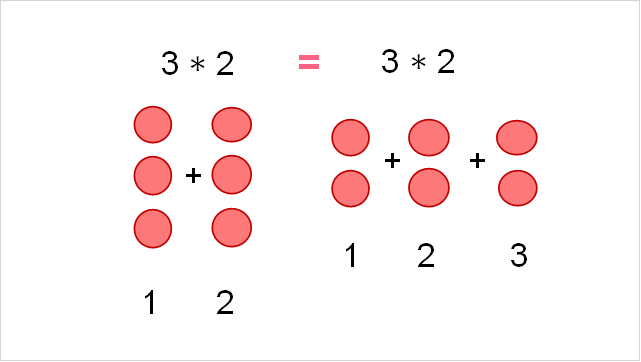
Associative Law
The associative law states that how you group numbers that have the same operation does not matter. Like the commutative law, this does not apply to subtraction and division. The associative law only applies when we have the same operation between multiple numbers.
Addition
In addition, the order in which you add each number does not matter no matter how you group them. Grouping numbers usually comes in the form of putting parentheses around them. This can be written as the following:


Multiplication
In multiplication, the order in which you multiply each number does not matter no matter how you group them. This can be written as the following:

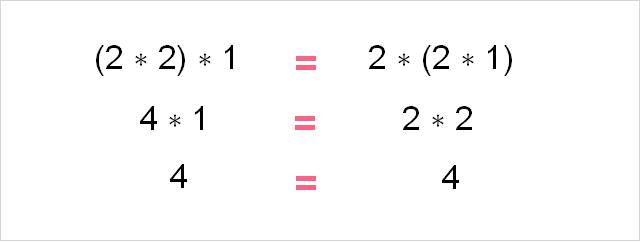
Distributive Law
The distributive law can be thought of as a combination of the other laws. It can be applied to:
- Multiplication
- Addition
- Subtraction
In order to understand the distributive law, we can look at the following image:

| Step 1 | You start with an operation between some numbers, here its addition | a + b |
| Step 2 | You multiply this operation with a number | (a+b) x c |
| Step 3 | You ‘distribute’ the c to every number inside the parenthesis | Distribute c to a and b |
| Step 4 | Add the result | ac + bc |
As an example, take a look at the image below.

Multiplicative Identity
A multiplicative identity sounds complicated, but is really just a number that, when multiplied, leaves the original number as it is. For rational numbers, the multiplicative identity is 1.
\[
b * 1 = b
\]
As you can see, when you multiply any rational number by 1, it is simply itself. See an example below.
\[
15 * 1 = 15
\]
Multiplicative Inverse
A multiplicative inverse is the reciprocal of a number. To understand what a reciprocal is, take the image below as an example.

As you can see, a reciprocal can be thought of the inverse of a number. Since 3 can be written as  , it’s inverse is simply
, it’s inverse is simply  . Notice that when a number and its inverse are multiplied together, they equal to one. Take a look at some examples below.
. Notice that when a number and its inverse are multiplied together, they equal to one. Take a look at some examples below.
| Number | Reciprocal | Result |
| 5 |  | 5 *  = 1 = 1 |
 |  |  * *  = 1 = 1 |
| 4 |  | 4 *  = 1 = 1 |













