Chapters
In this article, we will discuss what is an inverse proportion with examples. So, let us get started.

What is a Proportion?
A proportion says that the two ratios
and
are equal to each other.
Either two quantities are directly proportional or inversely proportional to each other. In other words, there are two types of proportions: direct proportion and inverse proportion. In the next section, we will discuss both the proportions in detail.
Direct vs Inverse Proportion
The relationship between two quantities or variables is depicted by a direct or inverse proportion. We also call these quantities "directly proportional" or "inversely proportional" to each other. The symbol 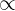 is used to depict the proportionality of the quantities.
is used to depict the proportionality of the quantities.
For instance, if we say that x is directly proportional to y, then we mathematically write it as:
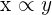
If we say that x is inversely proportional to y, then we write this fact in mathematical notation as:

The relationship between the variables x and y are controlled by some rules of proportionality. You can see that in both cases the value of x changes with respect to the value of y or when the value of y changes, x also changes.
Two quantities are directly proportional to each other when one quantity is multiple of another.
For example, if one 1 kilogram is equal to 1000 grams, then 8 kilograms will be equal to 8 x 1000 = 8000 grams. Hence, we can say that the units kilograms and grams are directly proportional to each other because when one quantity increases, the other quantity increases too. Similarly, if any of these two quantities decreases, then the other quantity decreases too. In other words, both quantities are directly related to each other.
Inverse proportion can be defined as:
Two quantities are inversely proportional to each other, if the increase in one quantity causes a decrease in the other quantity and vice versa
For example, consider an equation  . This equation shows that x is inversely proportional to y because when y increases x decreases, and when y decreases x increases.
. This equation shows that x is inversely proportional to y because when y increases x decreases, and when y decreases x increases.
In the next section, we will solve a couple of examples related to inverse proportion.
Example 1
3 painters complete painting a house in 12 hours. How many hours will 6 workers take?
Solution
By reflecting on the question, you can clearly guess that it is the scenario of inverse proportion because if the painters are fewer, they will take more time. Conversely, if the painters are more, they will take less time. In other words, the number of hours and the number of painters is inversely proportional to each other.
Make an equation of inverse proportion like this:
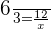


Hence, 6 painters will complete painting the house in 6 hours.
Example 2
It takes 12 hours to fill a water reservoir with water if 21 liters are poured into it per minute. How long will it take to fill the reservoir if 8 liters of water are poured into it per minute?
Solution
Number of hours required to fill water at the rate of 21 liters per minute = 12
Number of hours required to fill the water at the rate of 8 liters per minute = x
This is also a clear scenario of inverse proportion because when the rate of water will increase the time taken to fill the reservoir will decrease and vice versa. We can write the equation of the inverse proportion as:


It will take 31 hours 30 minutes to fill the reservoir if the flow of the water is 8 liters per minute.
Example 3
Two people take 15 minutes to clean the room. How many minutes will three people take to clean the same room?
Solution
Time taken by 2 people to clean the room = 15 minutes
Time taken by 3 people = x
This is the case of inverse proportionality because the more the people are, the less time it would take to clean the room. Now, we will write this scenario in the following form:


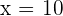
Hence, 3 people will take 10 minutes to clean the same room.
Example 4
10 students take 8 hours to decorate their classroom. How many hours will 5 students take to decorate the same classroom?
Solution
Number of hours taken by 10 students to decorate the classroom = 8 hours
Number of hours taken by 5 students to decorate the same classroom = x
This is the case of inverse proportionality because when the number of students will decrease, the time taken to decorate the classroom will increase and vice versa. We will write this scenario in the form of inverse proportion as:



Hence, 5 students will take 16 hours to decorate the same classroom.
Example 5
8 students take 2 hours to complete the work on a project. How many hours will 5 students take to complete the work on the same project?
Solution
Number of hours taken by 8 students to complete the project = 2 hours
Number of hours taken by 5 students to complete the project = x
This is the case of inverse proportionality because when the number of students will decrease, the time taken to complete the project will increase and vice versa. We will write this scenario in the form of inverse proportion as:

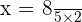

Hence, 5 students will take 3.2 hours to complete the project. You can convert the decimal part of the answer into minutes by multiplying 0.2 by 60 to get 12. Hence, 5 students will take 3 hours 12 minutes to complete the project.
Example 6
It takes 18 hours to cover a distance if the car travels at 50 miles per hour. How many hours will it take to cover the same distance if the speed of the car is increased to 75 miles per hour?
Solution
Number of hours required to cover a distance at the speed of 50 miles per hour = 18
Number of hours required to cover the same distance at the speed of 75 miles per hour = x
This is also a clear scenario of inverse proportion because when the speed of the car will increase, the time taken to travel the distance will decrease. Similarly, if the speed will decrease, the time taken to cover the distance will increase. We can write the equation of the inverse proportion as:


It will take 12 hours to cover the same distance if the car travels at the speed of 75 miles per hour.













