Chapters
In this article, we will discuss what is a direct proportion with examples. So, let us get started.

What is a Proportion?
A proportion reflects an equation which says that the two ratios for instance
and
are equal to each other.
The mathematical notation of the proportion is:
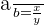
We can have either direct or inverse proportions. It means that there are two types of proportion, named direct and inverse proportions. In the next section, we will discuss direct proportion in detail.
Direct Proportion vs Inverse Proportion
We know that a proportion depicts a relationship between two quantities or variables. This relationship is either direct or inverse. In other words, we can say that either two quantities are directly proportional or inversely proportional to each other. 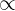 is used to reflect the proportionality between different quantities.
is used to reflect the proportionality between different quantities.
For instance, if we say that a is directly proportional to b, then in mathematical notation we can write it as:

Consider another scenario in which the variable a is inversely proportional to b. We can write it as:
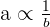
Some proportionality rules govern the relationship between the quantities a and b. Whether two variables are directly or inversely proportional to each other, the change in either variable causes a shift in another variable.
So far, we have discussed the proportionality between different quantities in detail. Let us now define direct proportion formally:
If one quantity is a multiple of another quantity, then we say that the two quantities are directly proportional to each other
Or
If there are two quantities and an increase in one quantity causes an increase in another quantity or a decrease in one quantity causes a decrease in another quantity, then we can say that the two quantities are directly proportional to each other
For example, the speed of the car and the distance covered are directly proportional to each other because the greater the speed of the car is, the more distance the car can travel. So, we can reflect this relationship as:
Distance 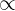 Speed
Speed
Let us take another example of a greater unit kilometer. In one kilometer, there are 1000 meters. Hence, 5 kilometers are equal to 5000 meters. Hence, we can say that kilometers and meters are directly proportional to each other because when one quantity increases, the other increases too. Similarly, if one quantity decreases, the other decreases too. Therefore, these two quantities are directly proportional to each other.
Two quantities are inversely proportional to each other, if an increase in one quantity causes a decrease in the other quantity or a decrease in one quantity causes an increase in another quantity
For instance, consider an equation 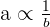 . This equation shows that the variable a is inversely proportional to b because when a will increase, the value of b will decrease and vice versa.
. This equation shows that the variable a is inversely proportional to b because when a will increase, the value of b will decrease and vice versa.
In the next section, we will solve a couple of examples related to direct proportion.
Example 1
3 pounds of a pineapple cake costs \ \propto
\propto 66
66
Cost of 5 pounds cake = x
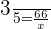


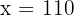
Hence, the cost of 5 pound cake will be 110 dollars.
Example 2
8 kg of sugar costs \ \propto
\propto 48
48
Cost of 10 kg sugar = x

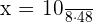
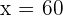
Hence, the cost of 10 kg of sugar will be 60 dollars.
Example 3
A car travels 300 miles at a constant speed in 6 hours. How many miles will be travelled in 4 hours?
Solution
In this example, the distance and time are directly proportional to each other because the greater the distance will be, the more time it will require to cover the distance. Similarly, the lesser the distance is, the less time it will take to cover that. Mathematically, we can write it as:
Distance 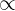 Time
Time
Now, let us write the proportionality equation using the information from this example.
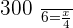
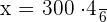

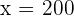
Hence, in four hours the car will travel 200 miles.
Example 4
A grandmother distributes 660 dollars among three children who are 9, 10, and 14 years of age. Suppose she distributes the money in proportion to the ages of the grandchildren. How much money will each grandchild receive?
Solution
Suppose three children receive x, y, and z amounts respectively. We can write this information in the form of proportionality equation as:

Here, 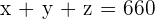
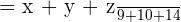
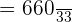
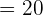
Each grandchild will receive:


 dollars
dollars


 dollars
dollars
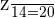

 dollars
dollars
Hence, the three children will receive 180, 200, and 280 dollars.
Example 5
A car travels 420 miles at a constant speed in 7 hours. In how many hours will it cover 180 miles of distance?
Solution
In this example, the distance and time are directly proportional to each other because the greater the distance will be, the more time it will require to cover the distance. Similarly, the lesser the distance is, the less time it will take to cover that. Mathematically, we can write it as:
Distance 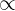 Time
Time
Now, let us write the proportionality equation using the information from this example.
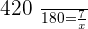


Hence, it can cover 180 miles in 3 hours.













