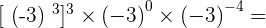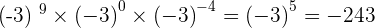Chapters
Exercise 1
Write the following integers in increasing order, represent them graphically, and calculate the additive inverse and absolute values of the numbers:
Exercise 2
Write the following integers graphically in increasing order and calculate the additive inverse and absolute values.
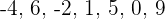
Exercise 3
Remove the common factor in the following expressions:
1. 
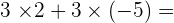
2. 
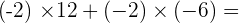
3. 
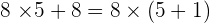
4. 
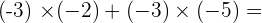
Exercise 4
Calculate:
1
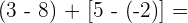
2
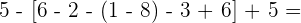
3
4
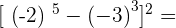
5
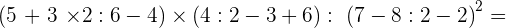
6
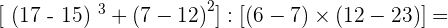
Exercise 5
Calculate:
1
2
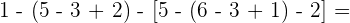
3
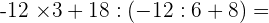
Exercise 6
Solve, if it exists:
1
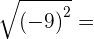
2
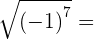
3
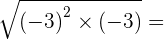
4
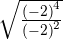
5
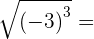
6
Exercise 7
Calculate:
1
2
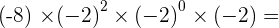
3
4
5
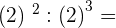
6
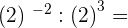
7
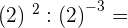
8
9
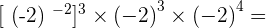
10
Exercise 8
Calculate:
1
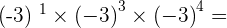
2
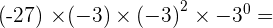
3
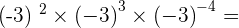
4
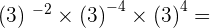
5
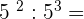
6
7
8
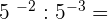
9
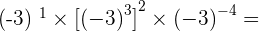
10
Solution of exercise 1
Write the following integers in increasing order, represent them graphically, and calculate the additive inverse and absolute values of the numbers:
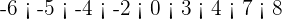
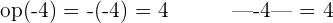
Solution of exercise 2
Write the following integers graphically in increasing order and calculate the additive inverse and absolute values.
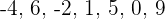
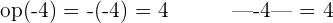
Solution of exercise 3
Remove the common factor in the following expressions:
1.
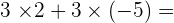
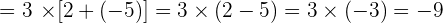
2.
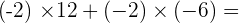
3.
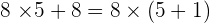
4.
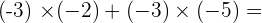
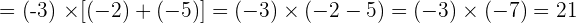
Solution of exercise 4
Calculate:
1
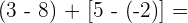
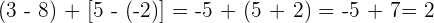
2
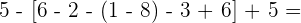
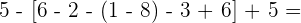
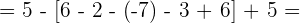
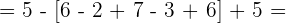
3
4
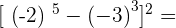
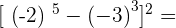
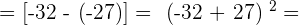
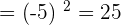
5
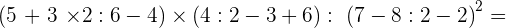
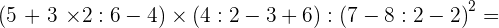
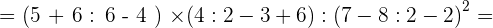
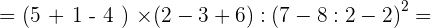
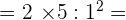
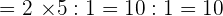
6
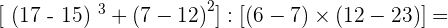
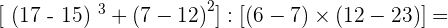
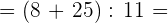
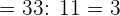
Solution of exercise 5
Calculate:
1
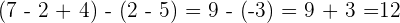
2
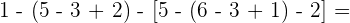
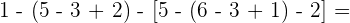
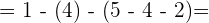
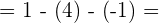
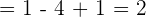
3
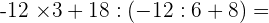−12 · 3 + 18 : (−12 : 6 + 8) =
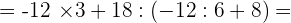
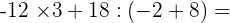
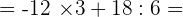
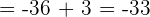
4
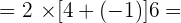
5
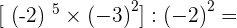
6
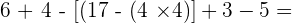
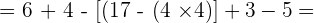
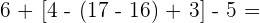
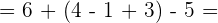
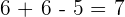
Solution of exercise 6
Solve, if it exists:
1
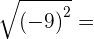
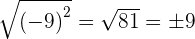
2
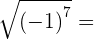
no solution
3
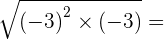
no solution
4
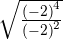
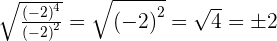
5
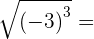
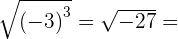no solution
6
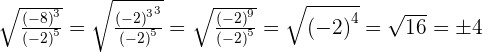
Solution of exercise 7
Calculate:
1
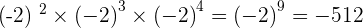
2
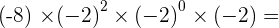
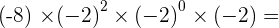
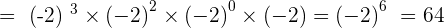
3
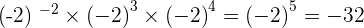
4
5
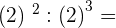
6
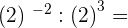
7
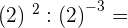
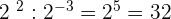
8
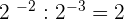
9
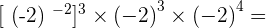
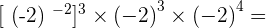
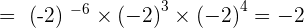
10
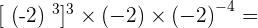
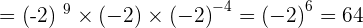
Solution of exercise 8
Calculate:
1
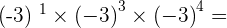
2
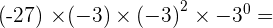
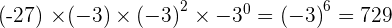
3
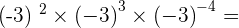
4
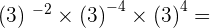
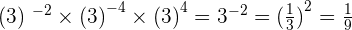
5
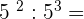
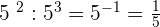
6
7
8
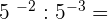
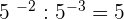
9
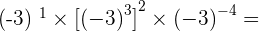
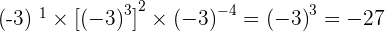
10
Did you like this article? Rate it!
Loading...
