Like other numbers, you can also use mathematical operations on integers. However, there are four mathematical operations that you can use which are addition, subtraction, multiplication, and division but in this lesson, we will talk about addition operation only.
Although adding integers isn't difficult, it is the same as adding two numbers but there are some differences. Integers are also negative as well as positive numbers. Their signs matter a lot irrespective of mathematical operation.
1. If the addends have the same sign, add the absolute values and the result will also have the same sign.
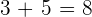

In the first example, both numbers have the same signs (which is plus). Therefore we performed the addition operation. In the next example, there are negative signs on both numbers yet we applied the addition operation but the answer is also written in the negative form. All you need to remember that if the signs are the same, addition operation is applied and the resultant number will also have the same sign as you can see in the second example.
2. If the addends have different signs, subtract the absolute values (subtract the lowest from the largest) and the result is in the same sign as the number of the largest absolute value.
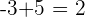

In the first example, since  is lesser than
is lesser than  and
and  has a negative sign meaning the resultant number will be positive. Now you need to apply the basic mathematical operation but there is a twist. We wanted to add them but both numbers have different directions which means that we need to apply subtraction operation, not addition operation. In the second example, this time,
has a negative sign meaning the resultant number will be positive. Now you need to apply the basic mathematical operation but there is a twist. We wanted to add them but both numbers have different directions which means that we need to apply subtraction operation, not addition operation. In the second example, this time,  has a negative sign and of course,
has a negative sign and of course,  is greater than
is greater than  hence the resultant number will also have a negative sign.
hence the resultant number will also have a negative sign.

Properties of the Addition of Integers
There are some properties of adding integers that you should know. Below are all the properties:
Property No.1: Closure
This property tells that if you add two integers this will result in a new number which will also be an integer.
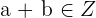
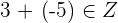
Property No.2: Associative
It doesn't matter what way you group, it will always result in the same. In simple words, the way in which the addends are grouped does not change the result.


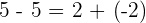
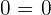
Property No.3: Commutative
When you are adding two integers, the order doesn't change the sum.


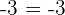
Property No.4: Additive Identity
Adding zero will not change the overall result because zero is a whole number. If you add zero to any number, it will always give the same number.
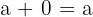
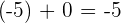
Property No.5: Additive Inverse
If you add two same numbers with opposite signs will always result in zero.
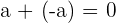
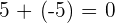
However, if you take the opposite of an integer (which is also opposite), it will be equal to the absolute value of the same number.














