Chapters
When you multiply two numbers, you will get a number, however, if you generate a series of a fixed number with variable numbers then we call it multiples. To understand multiples, you should know the concept of multiplication. For example, we have a number a and a number b. When we multiply both numbers, we will get another number which is the multiple of a and b. It is not necessary that multiplication of two same or different numbers will result in a different number, it can be the same number.
Let's pick up a random number which is 18. The number 18 has different multiples such as 
, 
, 
, 
, 
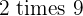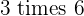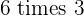, and 
. A natural multiple is obtained when a natural number is multiplied by another natural number.
Multiples of 2
 |  |  |  |  |
 |  |  |  |  |
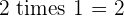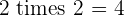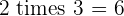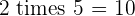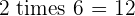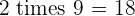Multiples of 3
 |  |  |  |  |
 |  |  |  |  |
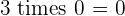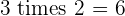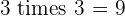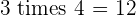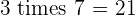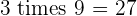Multiples of 4
 |  |  |  |  |
 |  |  |  |  |
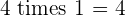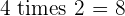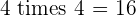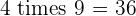Multiples of 5
 |  |  |  |  |
 |  |  |  |  |
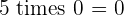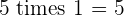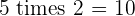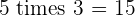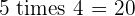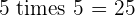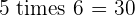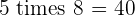Multiples of 6
 |  |  |  |  |
 |  |  |  |  |
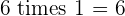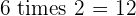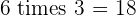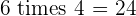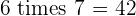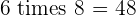Multiples of 7
 |  |  |  |  |
 |  |  |  |  |
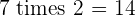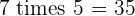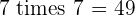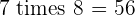Multiples of 8
 |  |  |  |  |
 |  |  |  |  |
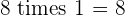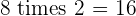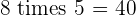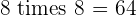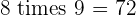Multiples of 9
 |  |  |  |  |
 |  |  |  |  |
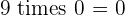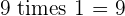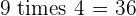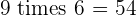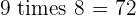Properties of the Multiples of a Number
Property no.1
Any number, except 0, is a multiple of itself and one.
Property no.2
Zero is a multiple of all numbers.
Property no.3
Any number, except zero, has infinite multiples.
Property no.4
If a number, a, is a multiple of b, the division between a and b is exact.
Property no.5
The sum of several multiples of a number is another multiple of that number.
Property no.6
The difference of two multiples of a number is another multiple of that number.
Property no.7
If a number is a multiple of another, and this number is a multiple of a third one, the first number is a multiple of the third one.
Property no.8
If a number is a multiple of another, all the multiples of the first number are also multiples of the second.
Find more Maths tutors near me here on Superprof.
Did you like this article? Rate it!
Loading...
