Chapters
- Exercise 1 - Standard Form
- Exercise 2 - Addition and Subtraction and the Complex Plane
- Exercise 3 - Multiplication, Modulus and the Complex Plane
- Exercise 4 - Powers of (1+i) and the Complex Plane
- Exercise 5 - Opposites, Conjugates and Inverses
- Exercise 6 - Reference Angles
- Exercise 7- Division
- Exercise 8 - Special Triangles and Arguments
- Exercise 9 - Polar Form of Complex Numbers
- Exercise 10 - Roots of Equations
- Exercise 11 - Powers of a Complex Number
- Exercise 12 - Complex Roots
- Solutions for Exercises 1-12
- Solutions for Exercise 1 - Standard Form
- Solutions for Exercise 2 - Addition and Subtraction and the Complex Plane
- Solutions for Exercise 3 - Multiplication, Modulus and the Complex Plane
- Solutions for Exercise 4 - Powers of (1+i) and the Complex Plane
- Solutions for Exercise 5 - Opposites, Conjugates and Inverses
- Solutions for Exercise 6 - Reference Angles
- Solutions for Exercise 7 - Division
- Solutions for Exercise 8 - Special Triangles and Arguments
- Solutions for Exercise 9 - Polar Form
- Solutions for Exercise 10 - Roots of Equations
- Solutions for Exercise 11 - Powers of a Complex Number
- Solutions for Exercise 12 - Complex Roots

Exercise 1 - Standard Form
Write these Complex numbers in Standard Form
a. 
b. 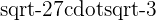
c.
d. 
Exercise 2 - Addition and Subtraction and the Complex Plane
Perform the addition or subtraction and draw the new Complex number
a. 
b. 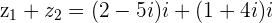
c. 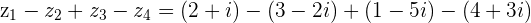
d. 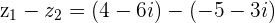
Exercise 3 - Multiplication, Modulus and the Complex Plane
Perform the multiplication, draw the new Complex number and find the modulus
a. 
b. 
c. 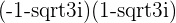
d. 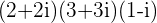
e. 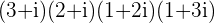
Exercise 4 - Powers of (1+i) and the Complex Plane
Perform the following calculations on 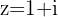 and state the position in the plane, how much you rotated and the modulus at each step
and state the position in the plane, how much you rotated and the modulus at each step
a. 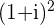
b. 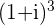
c. 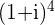
d. 
e. 
f. 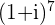
g. 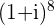
Exercise 5 - Opposites, Conjugates and Inverses
Find  and
and 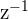 (if they exist) for each of the following
(if they exist) for each of the following
a. 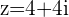
b. 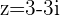
c. 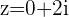
d. 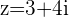
e. 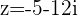
f. 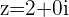
Exercise 6 - Reference Angles
Find the fractions that make the equations true
a. What is 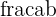 in the equation
in the equation 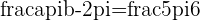 ?
?
b. What is 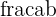 in the equation
in the equation 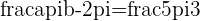 ?
?
c. What is 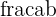 in the equation
in the equation 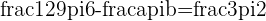 ?
?
Exercise 7- Division
Perform the division
a. 
b. 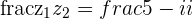
c. 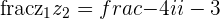
d. 
e. 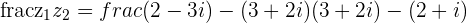
Exercise 8 - Special Triangles and Arguments
Use special triangles to find a Complex number that has each of these arguments
a. 
b. 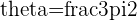
c. 
d. 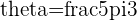
e. 
f. 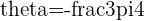
g. 
Exercise 9 - Polar Form of Complex Numbers
Determine the Polar Form for each of these Complex numbers
a. 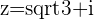
b. 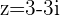
c. 
d. 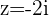
e. 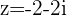
f. 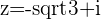
g. 
Exercise 10 - Roots of Equations
Solve for the roots of these equations
a. 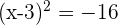
b. 
c. 
Exercise 11 - Powers of a Complex Number
Calculate the following numbers
a. 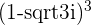
b. 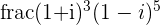
Expand 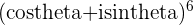 to find
to find
c. 
d. 
If 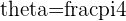 find the explicit answer for
find the explicit answer for
e. 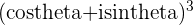
f. 
Exercise 12 - Complex Roots
a. Calculate the 4th roots of unity 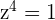
b. Calculate the 6th roots of unity 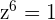
c. Calculate 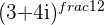
d. Calculate 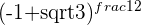
e. Use the Complex version of the Quadratic Formula to obtain the roots to the equation 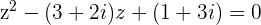
Solutions for Exercises 1-12
Solutions for Exercise 1 - Standard Form
Write these Complex numbers in Standard Form
a. 
 then
then

b. 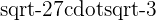
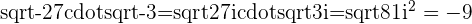
c.

d. 

Solutions for Exercise 2 - Addition and Subtraction and the Complex Plane
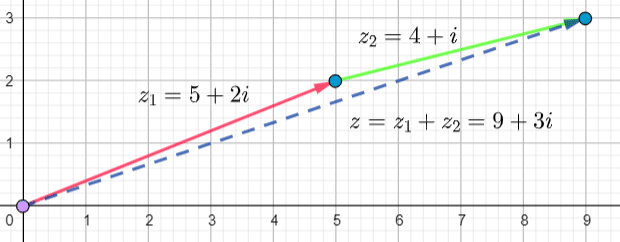
Perform the addition or subtraction and draw the new Complex number
a. 
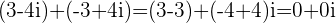
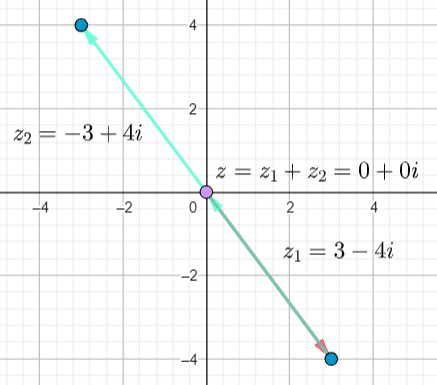
b. 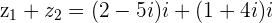
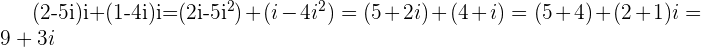
c. 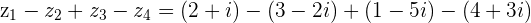
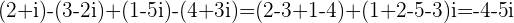
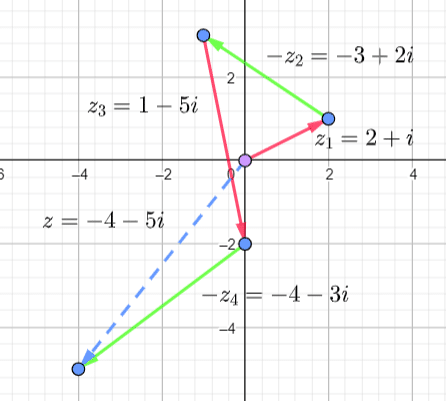
d. 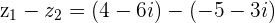


Solutions for Exercise 3 - Multiplication, Modulus and the Complex Plane
Perform the multiplication, draw the new Complex number and find the modulus
a. 
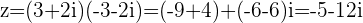
modulus 
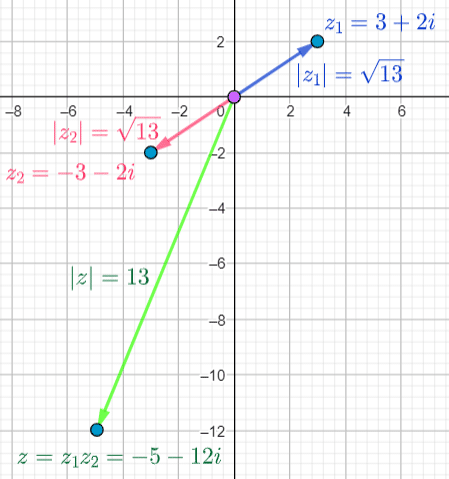
b. 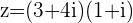

modulus 

c. 
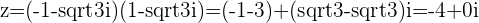
modulus 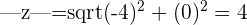

d. 

modulus 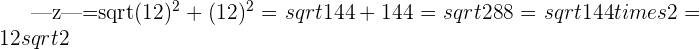

e. 

modulus 
Solutions for Exercise 4 - Powers of (1+i) and the Complex Plane
Perform the following calculations on  and state the position in the plane, how much you rotated and the modulus at each step
and state the position in the plane, how much you rotated and the modulus at each step
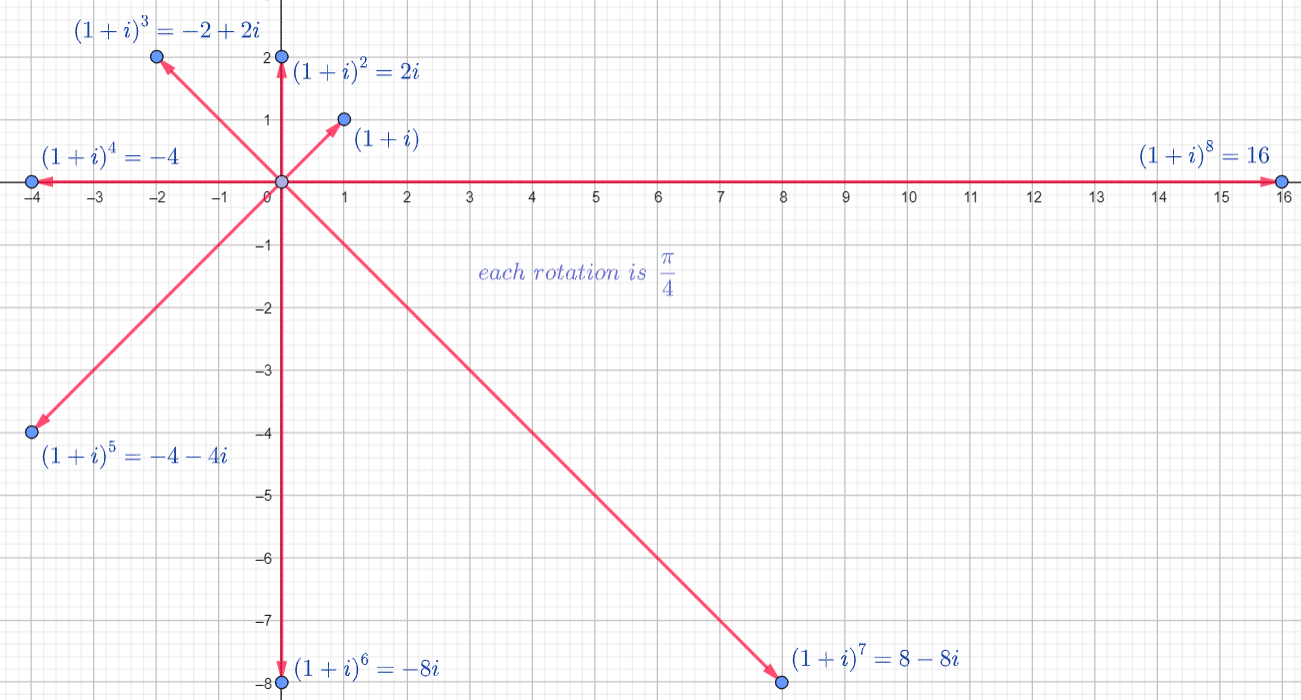
a. 
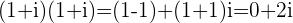
rotation and position: 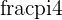 rotation to the positive y-axis at point
rotation to the positive y-axis at point 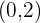
all of the rotations will be 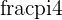 radians
radians
modulus: 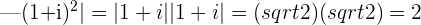
b. 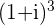

location: halfway between the positive y-axis and negative x-axis at the point 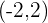
angle: 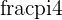
modulus: 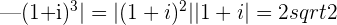
c. 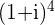
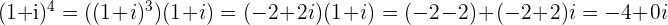
location: on the negative x-axis at the point 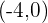
modulus: 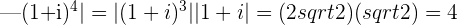
d. 

location: halfway between the negative x-axis and the negative y-axis at the point 
modulus: 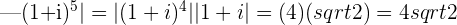
e. 
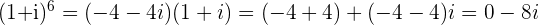
location: on the negative y-axis at the point 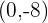
modulus: 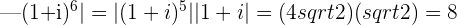
f. 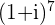

location: halfway between the negative y-axis and the positive x-axis at the point 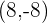
modulus: 
g. 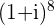
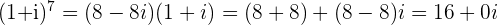
location: the positive x-axis at the point 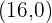
modulus: 
Solutions for Exercise 5 - Opposites, Conjugates and Inverses
Find  and
and 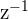 (if they exist) for each of the following
(if they exist) for each of the following
a. 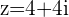
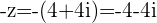
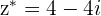

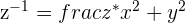
b. 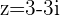
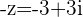


c. 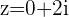
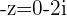
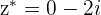

d. 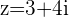


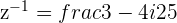
e. 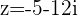
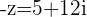


f. 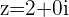



Solutions for Exercise 6 - Reference Angles
Find the fractions that make the equations true
a. What is 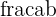 in the equation
in the equation 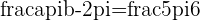 ?
?
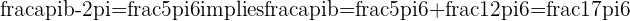
b. What is 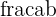 in the equation
in the equation 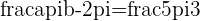 ?
?
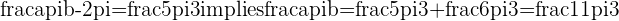
c. What is 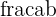 in the equation
in the equation 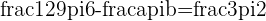 ?
?
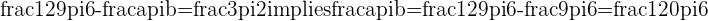
Solutions for Exercise 7 - Division
Perform the division
a. 


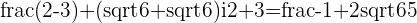
b. 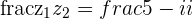

c. 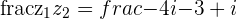
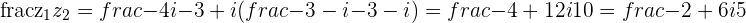
d. 
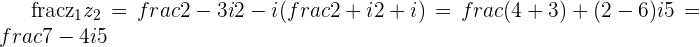
e. 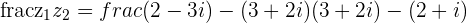

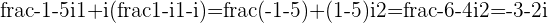
Solutions for Exercise 8 - Special Triangles and Arguments
Use special triangles to find a Complex number that has each of these arguments
a. 
Quadrant II with x negative and y positive
a 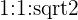 triangle for odd multiples of
triangle for odd multiples of 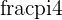
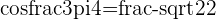 and
and 
 ,
, 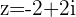 etc. any number with
etc. any number with 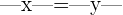
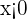 and
and 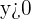
b. 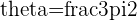
Negative y-axis with y negative
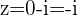 ,
, 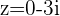 etc. any number with
etc. any number with  and
and 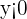
c. 
Quadrant I with x and y both positive
a  triangle with
triangle with 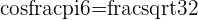 and
and 
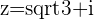 ,
, 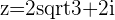 etc.
etc.
d. 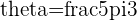
Quadrant IV with  and
and 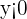
a  triangle with
triangle with 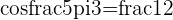 and
and 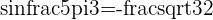
 ,
,  etc.
etc.
e. 
Quadrant III with both 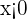 and
and 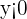
a  triangle with
triangle with 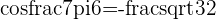 and
and 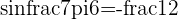
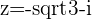 ,
, 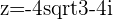 etc.
etc.
f. 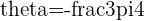
Quadrant III equivalent to angle 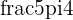 with both
with both 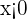 and
and 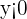
a 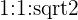 triangle with
triangle with  and
and 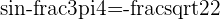
 ,
,  etc.
etc.
g. 
Quadrant III equivalent to angle  with
with 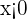 and
and 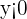
a  triangle with
triangle with 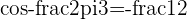 and
and 
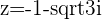 ,
, 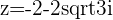
Solutions for Exercise 9 - Polar Form
Determine the Polar Form for each of these Complex numbers
a. 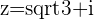
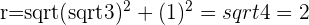

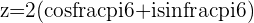
b. 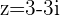
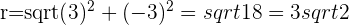
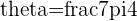

c. 
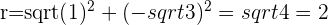
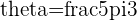

d. 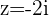
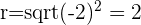
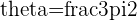
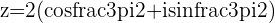
e. 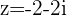
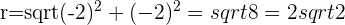
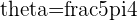
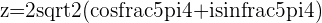
f. 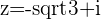

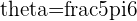
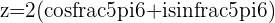
g. 

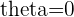 or
or 
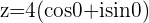 or
or 
Solutions for Exercise 10 - Roots of Equations
Solve for the roots of these equations
a. 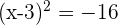
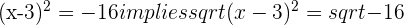
 and
and 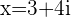 or
or 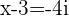 and
and 
solutions are 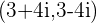
b. 
Expand 
Set the Real parts and the Imaginary parts of each side equal to each other
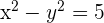 and
and 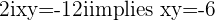
If we take the modulus of each side, we can obtain a expression for 

Now 
and 
Then 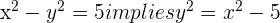 and
and 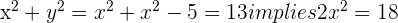 or
or 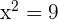 so
so
 with
with 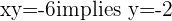 or
or  with
with 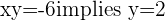
solutions 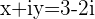 and
and 
with  or
or 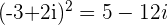
c. 

then 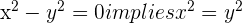 and
and 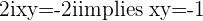
with 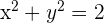 with
with 
then  with
with  or
or  with
with 
solutions 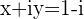 and
and 
with 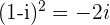 or
or 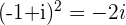
Solutions for Exercise 11 - Powers of a Complex Number
Calculate the following numbers
a. 
 which is equivalent to
which is equivalent to 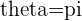
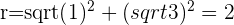
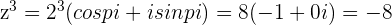
b. 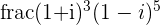
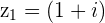 with
with 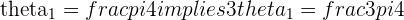 and
and 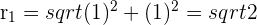
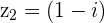 with
with 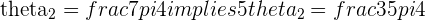 or
or 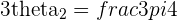 and
and 
Expand 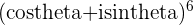 to find
to find
Binomial expansion for 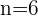 :
: 







c. 

d. 
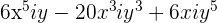
If 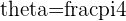 find the explicit answer for
find the explicit answer for
e. 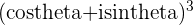
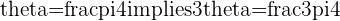
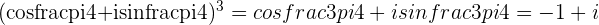
f. 

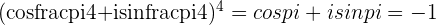
Solutions for Exercise 12 - Complex Roots
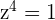
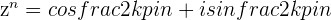
 where
where 
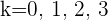




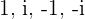 b.
b.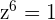
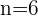 and
and 
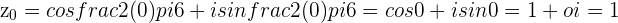
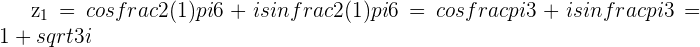

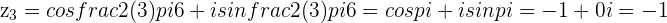
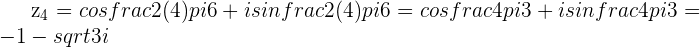
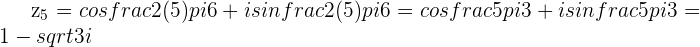
6th Roots of Unity: 
c. Calculate 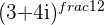
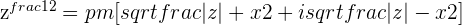


because
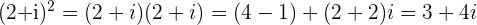 and
and 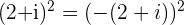
Calculate the roots of these equations
d. 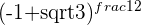
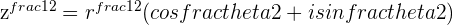
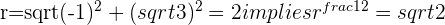
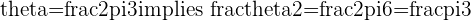
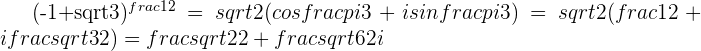
Use the Complex version of the Quadratic Formula to obtain the roots to the equation 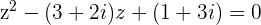
Quadratic Equation: 
Quadratic Formula: 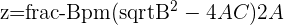
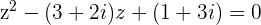 with
with 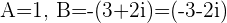 and
and 
then 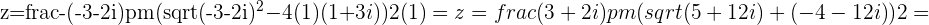

 and
and 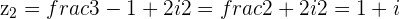













It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory