Temas
En el plano cartesiano el producto escalar —también llamado producto punto, o bien, producto interno— de dos vectores 
y 
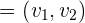es un número real positivo que corresponde al producto de sus módulos por el coseno del ángulo 
que forman
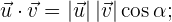
y en su representación analítica, equivale a la suma del producto de sus entradas coordenada a coordenada:
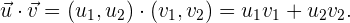
En el espacio cartesiano, la interpretación geométrica del producto escalar es la misma pues el ángulo corresponde al ángulo que se forma en el plano que contiene a los vectores. Además, el módulo de cada vector se calcula de la misma manera pero considerando una coordenada más. El módulo de un vector también se conoce como norma:
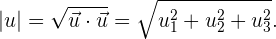
Por ejemplo, para el vector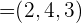 
el módulo es
¿Buscas una profesora de matematicas? Entra en Superprof, encuéntrala ¡y pide ya tu primera clase gratis!
Fórmulas del producto escalar en el espacio
Para dos vectores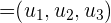 
y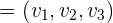 
en el espacio cartesiano, el producto escalar está dado por
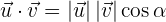
y su representación analítica como
Y, por tanto, el ángulo como
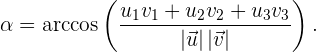
Ejemplo:
1 Hallar el producto escalar de los vectores 
2Calcular los módulos de los vectores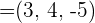 
y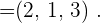 
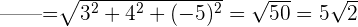
3Determinar el ángulo que forman los vectores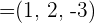 
y 
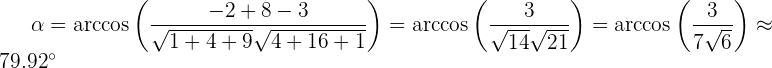
Generalizaciones del producto escalar en el espacio
Vectores ortogonales
Al igual que en el plano cartesiano, dos vectores son ortogonales si su producto escalar es cero, pues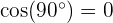 
. Así, si los vectores 
y 
son ortogonales entonces
Ejercicio:
Calcula los valores 
para que el vector 
sea ortogonal a los vectores 
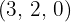y 
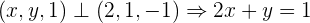
Así,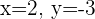 
.
Nota: Si los vectores y son paralelos, el ángulo que se forma es de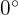 
y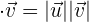 
, pues 
.
Nota: Si los vectores y forman un ángulo de 
, 
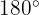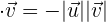pues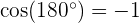 
.
Propiedades del producto escalar
1 Es conmutativo.
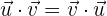
2 Es asociativo con respecto a la multiplicación por un escalar.
3 Es distributivo con respecto a la suma de vectores.
4 Hereda el ser positivo definido.
Interpretación geométrica del producto escalar
Dados dos vectores y considerando el plano que los contiene, puede interpretarse el producto escalar como el producto del módulo de un vector por el módulo de la proyección del otro vector sobre éste.
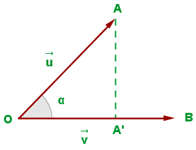
Como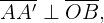 
aplicando las identidades trignométricas
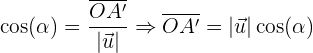
Entonces 
se define como la proyección del vector sobre el vector
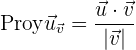
y el vector proyección de sobre a partir de un vector con módulo la unidad paralelo a :
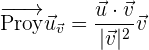
Ejercicio:
Dados los vectores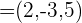 
y 
, calcula:
a) Los módulos de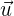 
y .
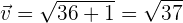
b) El producto escalar de 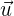y .
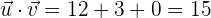
c) El ángulo que forman.
d) La proyección d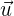e sobre .
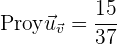
e) La proyección de 
sobre .
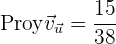
f) Calcula el valor de 
para que los vectores 
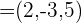y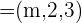 
sean ortogonales.
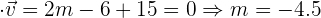
Cosenos directores de una base ortonormal
En una base ortonormal, se llaman cosenos directores del vector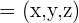 
a los cosenos de los ángulos que forma con cada uno de los vectores de la base. Si se consideran la base canónica 
, por ejemplo, se tiene que
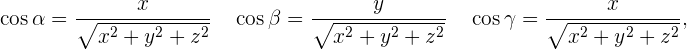
donde se cumple que
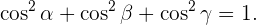
Ejercicio:
Determinar los cosenos directores del vector 
con respecto a la base canónica y verifica que su suma es 1.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
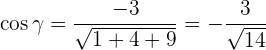
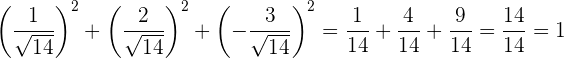
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo