Temas
Para sumar dos vectores se suman sus respectivas componentes.
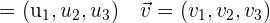
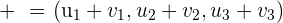
Ejemplos
1 Dados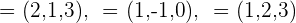 
, hallar el vector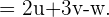 
Comenzamos por sustituir el valor de cada vector y sumar o restar sus respectivas componentes.
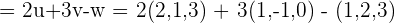
2 Dados los vectores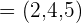 
y 
, hallar el módulo del vector 
.
Comenzamos por encontrar el valor de la resta de vectores, para luego sustituirlo en el módulo.
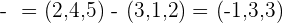
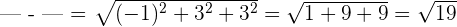
Propiedades de la suma de vectores
1 Asociativa
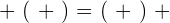
2 Conmutativa
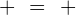
3 Elemento neutro
4Elemento opuesto
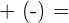
Producto de un número real por un vector
El producto de un número real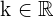 
por un vector 
es otro vector:
De igual dirección que el vector .
Del mismo sentido que el vector si 
es positivo.
De sentido contrario del vector si es negativo.
De módulo 
Las componentes del vector resultante se obtienen multiplicando por las componentes del vector.
Propiedades del producto de un número por un vector
1 Asociativa
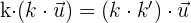
2 Distributiva respecto a la suma de vectores
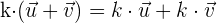
3 Distributiva respecto a los escalares
4 Elemento neutro
Ejemplo:
Dado 
determinar de modo que sea 
.
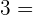Comenzamos por sustituir el valor del vector 
y luego realizamos las operaciones correspondientes.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Sean u = 2i − 3j y v = −4i + 6j. Encuentre: 4v − 6u , con su bosquejo
Al trasladar el punto A(2,4) dado el vector B(2-2) se obtiene?
Hola, de la matriz que calcularon la determinante no es =0.
Podrías señalar el ejercicio para rectificar por favor.
Calcular x²+1
Cómo resolver los ejercicios si están en kilómetros por ejemplo:
A= 300km b=4,000km C= 5,000km
Osea cuando sustituimos tenemos que poner √(X1,X2)² + (Y1,X2)²
O (X2,X1)² +(Y2,Y1)²
¿Cual de las dos?
Depende de que quieras obtener y que significa la expresión (X1,X2), la expresión √(X1,X2)² + (Y1,X2)² esta mal escrita si quieres encontrar una distancia.
24 4 70 NE
Vectores modelo