
Posiciones relativas de tres planos y matriz de coeficientes
Dados los planos:
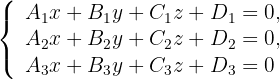
Y sean:
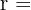 rango de la matriz de los coeficientes.
rango de la matriz de los coeficientes.
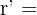 rango de la matriz ampliada.
rango de la matriz ampliada.
Las posiciones relativas de los tres planos vienen dadas por la siguiente tabla:
 |  | Posición | |||||||
|---|---|---|---|---|---|---|---|---|---|
 |  | 1. Planos secantes en un punto | |||||||
 |  |
|
| ||||||
 |  |
|
| ||||||
 |  |
|
| ||||||
 |  | 5. Planos coincidentes. |
¿Buscas clases de matematicas a domicilio? ¡Están en Superprof!
Planos secantes en un punto
Si 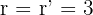 entonces los planos son secantes entre si y se cortan en un punto. Esto quiere decir que el sistema de ecuaciones formado por los tres planos es compatible determinado
entonces los planos son secantes entre si y se cortan en un punto. Esto quiere decir que el sistema de ecuaciones formado por los tres planos es compatible determinado
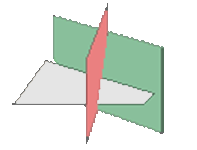
Si  y
y 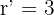 entonces se tienen dos posibilidades para la intersección de los tres planos
entonces se tienen dos posibilidades para la intersección de los tres planos
Planos secantes dos a dos
Si  y
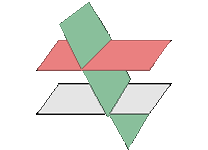
y 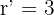 puede darse el cado que los planos se intersectan dos a dos formando una superficie primática. En este caso, el sistema de ecuaciones formado por los tres planos es incompatible
puede darse el cado que los planos se intersectan dos a dos formando una superficie primática. En este caso, el sistema de ecuaciones formado por los tres planos es incompatible

Dos planos paralelos y el tercero secante
Si  y
y 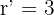 puede darse el caso de que dos planos sean paralelos y el tercero sea secante a los planos paralelos. En este caso, el sistema de ecuaciones formado por los tres planos es incompatible y dos filas de la matriz de los coeficientes son proporcionales.
puede darse el caso de que dos planos sean paralelos y el tercero sea secante a los planos paralelos. En este caso, el sistema de ecuaciones formado por los tres planos es incompatible y dos filas de la matriz de los coeficientes son proporcionales.
Si 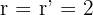 entonces se tienen dos posibilidades para la intersección de los tres planos
entonces se tienen dos posibilidades para la intersección de los tres planos
Planos secantes y distintos
Si 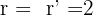 puede darse el caso de que los tres planos sean secantes y distintos pero los tres se intersecten en una misma recta. En este caso, el sistema de ecuaciones formado por los tres planos es compatible indeterminado.
puede darse el caso de que los tres planos sean secantes y distintos pero los tres se intersecten en una misma recta. En este caso, el sistema de ecuaciones formado por los tres planos es compatible indeterminado.
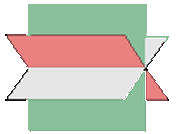
Dos planos coincidentes y uno secante
Si 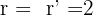 puede darse el caso de que dos planos. En este caso, el sistema de ecuaciones formado por los tres planos es compatible indeterminado y dos filas de la matriz ampliada son proporcionales.
puede darse el caso de que dos planos. En este caso, el sistema de ecuaciones formado por los tres planos es compatible indeterminado y dos filas de la matriz ampliada son proporcionales.

Si 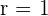 y
y  entonces se tienen dos posibilidades para la intersección de los tres planos
entonces se tienen dos posibilidades para la intersección de los tres planos
Planos paralelos y distintos dos a dos
Si 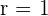 y
y  puede darse el caso de que los tres planos sean paralelos y distintos dos a dos. En este caso, el sistema de ecuaciones formado por los tres planos es incompatible.
puede darse el caso de que los tres planos sean paralelos y distintos dos a dos. En este caso, el sistema de ecuaciones formado por los tres planos es incompatible.

Planos paralelos y dos coincidentes
Si 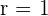 y
y  puede darse el caso de que dos planos coincidan y sean paralelos al tercero. En este caso, el sistema de ecuaciones formado por los tres planos es incompatible y dos filas de la matriz ampliada son proporcionales.
puede darse el caso de que dos planos coincidan y sean paralelos al tercero. En este caso, el sistema de ecuaciones formado por los tres planos es incompatible y dos filas de la matriz ampliada son proporcionales.

Planos coincidentes
Si  entonces los tres planos coinciden entre si. En este caso, el sistema de ecuaciones formado por los tres planos es compatible indeteminado.
entonces los tres planos coinciden entre si. En este caso, el sistema de ecuaciones formado por los tres planos es compatible indeteminado.

Ejemplos resuletos de planos
Hallar la posición relativa de los planos:
1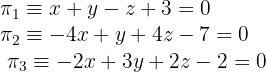
1Escribimos el sistema de ecuaciones

2Calculamos el rango de la matriz de coeficientes 

para ello calculamos el determinante de 
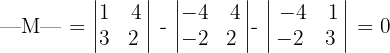
Calculamos el determinante de la submatriz 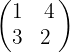
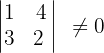
Así, 
3Calculamos el rango de la matriz de coeficientes extendida 
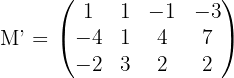
para ello calculamos el determinante de la submatriz
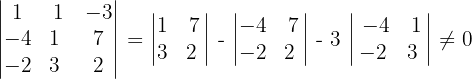
Así, 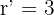 .
.
Como los planos no son paralelos entre si,  y
y 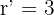 concluimos que los tres planos son secantes dos a dos y forman una superficie prismática
concluimos que los tres planos son secantes dos a dos y forman una superficie prismática
2
1Escribimos el sistema de ecuaciones

2Calculamos el rango de la matriz de coeficientes 

para ello calculamos el determinante de 
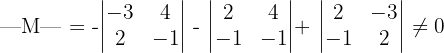
Así, 
3Calculamos el rango de la matriz de coeficientes extendida 
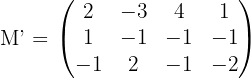
para ello calculamos el determinante de la submatriz  la cual sabemos que es distinto de cero. Así,
la cual sabemos que es distinto de cero. Así, 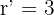 .
.
De esta forma se concluye que los tres planos se cortan en un punto
3
1Escribimos el sistema de ecuaciones
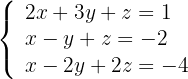
2Calculamos el rango de la matriz de coeficientes 
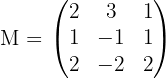
para ello calculamos el determinante de 

Calculamos el determinante de la submatriz 

Así, 
3Calculamos el rango de la matriz de coeficientes extendida 
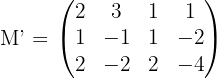
como la segunda y tercera fila son múltiplos entre si, cualquier submatriz de de tres por tres tiene determinante cero. Por ello calculamos el determinante de la submatriz

Así, 
De esta forma se concluye que el segundo y tercer plano son coincidentes y el primero es secante a ellos.
4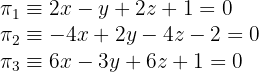
1Escribimos el sistema de ecuaciones

2Calculamos el rango de la matriz de coeficientes 

como las tres filas son múltiplos entres si, el determinante de esta matriz y la de todas sus submatrices de tamaño 2 es cero ello calculamos el determinante de 
Así, 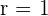
3Calculamos el rango de la matriz de coeficientes extendida 

como la primera y segunda fila son múltiplos entre si, cualquier submatriz de de tres por tres tiene determinante cero. Por ello calculamos el determinante de la submatriz

Así, 
De esta forma se concluye que el primer y segundo plano son coincidentes y el tercero es paralelo a ellos.











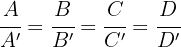



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Encontrar la ecuacion de la recta que pasa por los puntos (4,1) y (-2,4) ¿cual es la pendiente de la recta?
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =