Temas

Ecuación vectorial
En esta sección aprenderás a representar vectorialmente a todos los puntos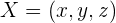 que pertenezcan a un plano llamado
que pertenezcan a un plano llamado  .
.
Para esto, necesitamos a un punto fijo del plano 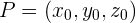 y a dos vectores con direcciones distintas
y a dos vectores con direcciones distintas 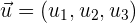 y
y 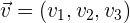 llamados vectores directores.
llamados vectores directores.
Los vectores  y
y  se denominan directores, ya que son los encargados de establecer las direcciones para generar a los puntos
se denominan directores, ya que son los encargados de establecer las direcciones para generar a los puntos  del plano
del plano  , dichos vectores se consideran en el plano.
, dichos vectores se consideran en el plano.
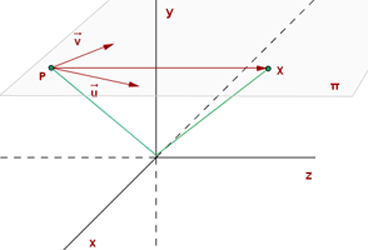
La construcción de la ecuación vectorial es la siguiente:
- Consideremos a
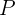 como un punto de referencia del plano
como un punto de referencia del plano 
- Consideramos a un vector en el plano
 que comienza en
que comienza en 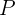 y termina en
y termina en  , dicho vector se puede construir de la siguiente manera
, dicho vector se puede construir de la siguiente manera

- Ahora, como
 y
y  también pertenecen a
también pertenecen a  y no tienen la misma dirección, es posible encontrar a escalares
y no tienen la misma dirección, es posible encontrar a escalares 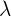 y
y 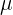 respectivamente, tales que sea posible crear a los vectores
respectivamente, tales que sea posible crear a los vectores  y
y 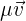 cuya suma sea
cuya suma sea 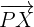 , es decir:
, es decir:
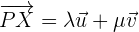
Entonces con esta igualdad ya es posible comenzar a desarrollar:

es decir:

llegando a la ecuación en su forma vectorial de los elementos del plano  :
:

Ecuaciones paramétricas del plano
Operando en la ecuación vectorial del plano llegamos a la igualdad:
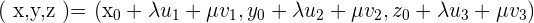
Esta igualdad se verifica si:
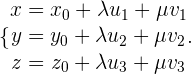
obteniendo así las ecuaciones paramétricas del plano.
Ecuación general o implícita del plano
Un punto  está en el plano
está en el plano  si tiene solución el sistema:
si tiene solución el sistema:
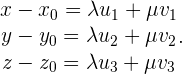
Este sistema tiene que ser compatible determinado en las incógnitas 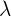 y
y 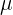 · Por tanto el determinante de la matriz ampliada del sistema con la columna de los términos independientes tiene que ser igual a cero.
· Por tanto el determinante de la matriz ampliada del sistema con la columna de los términos independientes tiene que ser igual a cero.

Desarrollamos el determinante.
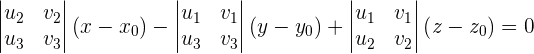
y si asignamos los valores:

Sustituimos:
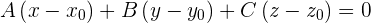
si desarrollamos ahora llegamos a:

y con la siguiente igualdad:
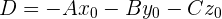
obtenemos la ecuación general de plano:

Vector normal
Vamos a construir la ecuación de un plano  usando otros elementos.
usando otros elementos.
Primero consideremos a un vector perpendicular al plano llamado vector normal 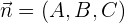 , y además a un punto fijo del plano
, y además a un punto fijo del plano 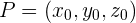
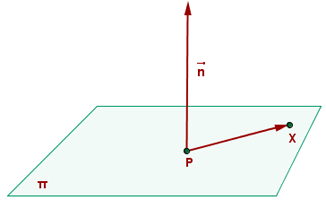
Sea 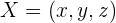 cualquier punto del plano.
cualquier punto del plano.
Construimos al vector dirigido de 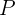 a
a  de la misma forma que anteriormente lo hicimos:
de la misma forma que anteriormente lo hicimos:

tal vector es perpendicular a  ya que pertenece a
ya que pertenece a  , y
, y  se consideró perpendicular a todo vector del plano.
se consideró perpendicular a todo vector del plano.
Entonces, por ser perpendiculares ambos vectores, su producto escalar vale cero:
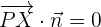
de este modo también se puede determinar la ecuación general del plano, a partir de un punto y un vector normal.
Ecuación canónica o segmentaria del plano
Sean ,
, 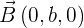 y
y  tres vectores en el espacio por donde pasa el plano
tres vectores en el espacio por donde pasa el plano  que se encuentran sobre los ejes de referencia.
que se encuentran sobre los ejes de referencia.

Construyamos a la ecuación de  en su forma canónica partiendo de su forma general.
en su forma canónica partiendo de su forma general.
Supongamos que tenemos a la ecuación en su forma general del plano  :
:

donde  ,
, 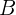 ,
, 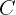 y
y  son todos números reales distintos de cero.
son todos números reales distintos de cero.
De la ecuación general restemos de ambos lados a  y posteriormente dividamos a ambos lados entre
y posteriormente dividamos a ambos lados entre  , quedando así el proceso:
, quedando así el proceso:
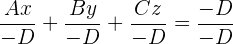
y si ahora estructuramos a las fracciones queda:
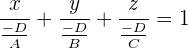
donde los denominadores coinciden exactamente con los valores  ,
,  y
y  de los vectores en el espacio que se mencionaron inicialmente, de esta manera si:
de los vectores en el espacio que se mencionaron inicialmente, de esta manera si:

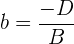
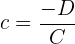
entonces ya tenemos a la ecuación de  en su forma canónica:
en su forma canónica:

 ,
, 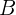 ,
, 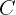 y
y  deben ser todos distintos de cero para evitar la indeterminación.
deben ser todos distintos de cero para evitar la indeterminación.
Ejercicios
1Hallar las ecuaciones paramétricas e implícitas del plano que pasa por el punto  y tiene como vectores directores a
y tiene como vectores directores a  y
y 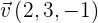 .
.
Como tenemos a un punto del plano y a sus dos vectores directores, simplemente sustituimos los valores en las ecuaciones en su forma paramétrica del plano, quedando entonces:
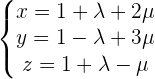
para que ahora conozcamos a la ecuación del plano en forma implícita, proponemos a la siguiente igualdad y resolvemos el determinante:
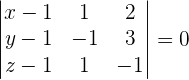
quedando de esta manera la ecuación que buscamos:

2Hallar las ecuaciones paramétricas e implícitas del plano que pasa por los puntos 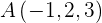 y
y 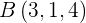 y contiene al vector
y contiene al vector  .
.
Primero consideremos al punto 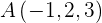 como el punto de referencia que pertenece al plano, posteriormente partiendo de
como el punto de referencia que pertenece al plano, posteriormente partiendo de  construyamos un vector dirigido hacia
construyamos un vector dirigido hacia 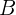 con la operación
con la operación 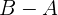 , teniendo así:
, teniendo así:

que se puede usar como el otro vector director, para que de esta manera podamos sustituir todo en la ecuaciones en su forma paramétrica del plano:
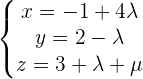
las cuales podemos usar para plantear la siguiente igualdad, y si desarrollamos el determinante obtenemos la ecuación en su forma general:
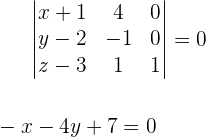
3Hallar las ecuaciones paramétricas e implícitas del plano que pasa por los puntos 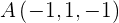 ,
,  y
y 
Consideremos al punto  como el punto de referencia que pertenece al plano, y partiendo de ahí construyamos a los dos vectores directores usando
como el punto de referencia que pertenece al plano, y partiendo de ahí construyamos a los dos vectores directores usando 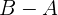 y
y 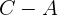 respectivamente:
respectivamente:
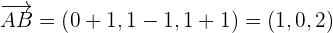
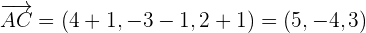
Entonces, usando a  como el punto del plano y a los vectores directores construidos, podemos establecer las ecuaciones del plano en su forma paramétrica:
como el punto del plano y a los vectores directores construidos, podemos establecer las ecuaciones del plano en su forma paramétrica:

y con esto ya podemos resolver el siguiente determinante (igualado con cero) y conocer a la ecuación del plano en su forma implícita o general:

4Sea 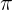 el plano de ecuaciones paramétricas:
el plano de ecuaciones paramétricas:
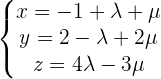
Se pide comprobar si los puntos 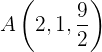 y
y 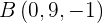 pertenecen al plano.
pertenecen al plano.
Primero encontremos a la ecuación del plano, desarrollando el determinante siguiente:
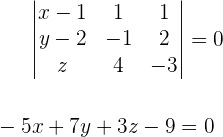
Ahora que ya tenemos la ecuación del plano, sustituyamos los puntos  y
y 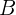 para saber si pertenecen al plano o no:
para saber si pertenecen al plano o no:
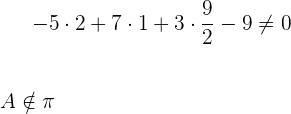

concluyendo que al darnos un resultado distinto de cero, entonces ninguno pertenece al plano.
5Hallar la ecuación segmentaria del plano que pasa por los puntos 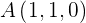 ,
, 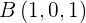 y
y 
Tomamos a el punto  como el punto de referencia que pasa por el plano y partiendo de él construimos a do vectores dirigidos tanto a
como el punto de referencia que pasa por el plano y partiendo de él construimos a do vectores dirigidos tanto a 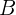 como a
como a 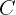 , que nos servirán como vectores directores:
, que nos servirán como vectores directores:
 .
.
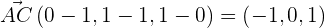 .
.
y con ésta información establecemos la siguiente igualdad para que al desarrollar el determinante conozcamos la ecuación del plano:

Ahora, restando 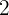 y dividiendo entre
y dividiendo entre 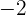 en ambos lados de la igualdad obtenemos la ecuación segmentaria:
en ambos lados de la igualdad obtenemos la ecuación segmentaria:
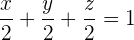 .
.
6Hallar la ecuación de la recta  , que pasa por el punto
, que pasa por el punto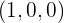 y es perpendicular al plano
y es perpendicular al plano  .
.
Por ser la recta perpendicular al plano, el vector normal del plano será el vector director de la recta que pasa por el punto 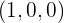 .
.
El vector normal del plano se puede obtener de los coeficientes de las variables, es decir  y con esto podemos representar a la ecuación de la recta con la siguiente forma:
y con esto podemos representar a la ecuación de la recta con la siguiente forma:
 .
.
7Hallar la ecuación del plano que pasa por el punto  y contiene a la recta de ecuación:
y contiene a la recta de ecuación:
 .
.
De la ecuación de la recta obtenemos un punto 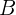 y el vector
y el vector  .
.
El punto 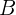 se puede obtener igualando con cero a cada uno de los denominadores para que la igualdad siempre se cumpla, de esta manera
se puede obtener igualando con cero a cada uno de los denominadores para que la igualdad siempre se cumpla, de esta manera  . El vector normal de la recta se obtiene de los denominadores
. El vector normal de la recta se obtiene de los denominadores 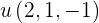 .
.
Ahora construimos al vector director usando 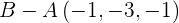 y podemos ocupar a u como el otro vector director:
y podemos ocupar a u como el otro vector director:
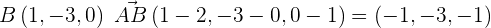 .
.
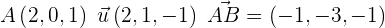 .
.
Significa que podemos encontrar a la ecuación del plano con el proceso que ya se ha mencionado, quedando el siguiente resultado  .
.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
encuentre una forma general de una ecuación de la recta q pasa por el punto A q satisfaga la condicion dada A (5, – 2)
a) paralelo al eje y
b) perpendicular al eje y
¿Cuál es el lugar geométrico descrito por la trayectoria de un avión que se mantiene sobre volando la ciudad de San José a una distancia constante de 5 km de la Torre de Juan Santamaría
Graficar y calcular la distancia y punto Medio de los siguientes P(1,1),Q (3,3)
Hallar la distancia y la pendiente de A(07)
B(2,1)
F(×)=5-2×
A= (7,7)
B= (-9,-6)
Ecuación explícita de la recta
una recta pasa por el punto (0,-5) formando con una x un ángulo de x=90° Hallar la ecuación de la recta
1. Hallar las ecuaciones paramétricas de la recta que pasa por A(3,-1,0) y su vector director sea
perpendicular a los vectores: w = y u =