1 El dueño de un bar ha comprado refrescos, cerveza y vino por importe de 500 € (sin impuestos). El valor del vino es 60 € menos que el de los refrescos y de la cerveza conjuntamente. Teniendo en cuenta que los refrescos deben pagar un IVA del 6%, por la cerveza del 12% y por El vino del 30%, lo que hace que la factura total con impuestos sea de 592.4 €, calcular la cantidad invertida en cada tipo de bebida.
 = Importe en € de los refrescos.
= Importe en € de los refrescos.
 = Importe en € de la cerveza.
= Importe en € de la cerveza.
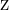 = Importe en € del vino.
= Importe en € del vino.
Entonces, tenemos el siguiente sistema de ecuaciones:

Simplificando la 3er ecuación del sistema anterior tenemos:

Para resolver este sistema de 3x3 podemos ocupar el método de Kramer, es decir,

Aplicando este método a nuestro sistema de ecuaciones tenemos:

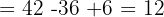

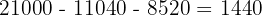

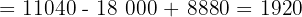

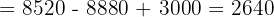
Finalmente, para encontrar los valores de cada incógnita:



Por lo tanto, las soluciones son:
x = 120 €
y = 160 €
z = 220 €
2 Una empresa tiene tres minas con menas de composiciones:
| Níquel (%) | Cobre (%) | Hierro (%) | |
|---|---|---|---|
| Mina A | 1 | 2 | 3 |
| Mina B | 2 | 5 | 7 |
| Mina C | 1 | 3 | 1 |
¿Cuántas toneladas de cada mina deben utilizarse para obtener 7 toneladas de níquel, 18 de cobre y 16 de hierro?
Comenzamos definiendo las variables a utilizar:
 = nº de toneladas de la mina A.
= nº de toneladas de la mina A.
 = nº de toneladas de la mina B.
= nº de toneladas de la mina B.
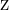 = nº de toneladas de la mina C.
= nº de toneladas de la mina C.
Entonces, tenemos el siguiente sistema de ecuaciones:

Simplificando el sistema anterior tenemos:

Para resolver este sistema de 3x3 podemos ocupar el método de Kramer, es decir,

Aplicando este método a nuestro sistema de ecuaciones tenemos:



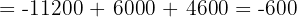

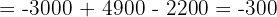

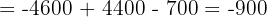
Finalmente, para encontrar los valores de cada incógnita:



Por lo tanto, las soluciones son:
x = 200 t
y = 100 t
z = 300 t
3 La edad de un padre es doble de la suma de las edades de sus dos hijos, mientras que hace unos años (exactamente la diferencia de las edades actuales de los hijos), la edad del padre era triple que la suma de las edades, en aquel tiempo, de sus hijos. Cuando pasen tantos años como la suma de las edades actuales de los hijos, la suma de edades de las tres personas será 150 años. ¿Qué edad tenía el padre en el momento de nacer sus hijos?
 = Edad actual del padre.
= Edad actual del padre.
 = Edad actual del hijo mayor.
= Edad actual del hijo mayor.
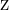 = Edad actual del hijo menor.
= Edad actual del hijo menor.
Relación actual: 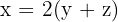
Hace y − z años: 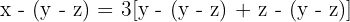
Dentro de y + z: 
Entonces, tenemos el siguiente sistema de ecuaciones:

Para resolver este sistema de 3x3 podemos ocupar el método de Kramer, es decir,

Aplicando este método a nuestro sistema de ecuaciones tenemos:

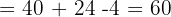

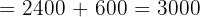

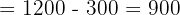

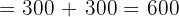
Finalmente, para encontrar los valores de cada incógnita:



Por lo tanto,
Al nacer los hijos, el padre tenía  y
y  años, respectivamente.
años, respectivamente.
4 Se venden tres especies de cereales: trigo, cebada y mijo.
Cada volumen de trigo se vende por 4 €, el de la cebada por 2 € y el de mijo por 0.5 €.
Si se vende 100 volúmenes en total y si obtiene por la venta 100 €, ¿cuántos volúmenes de cada especie se venden?
 = Volumen de trigo.
= Volumen de trigo.
 = Volumen de cebada.
= Volumen de cebada.
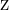 = Volumen de mijo.
= Volumen de mijo.
Entonces, tenemos el siguiente sistema de ecuaciones:

Multiplicando la segunda ecuación por 2 y reescribiendo el sistema, tenemos

Para resolver este sistema de 2x2 podemos ocupar el método de Kramer, es decir,

Aplicando este método a nuestro sistema de ecuaciones tenemos:


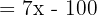

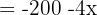
Tenemos que dos de las variables son dependientes de la variable x
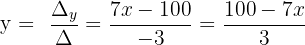
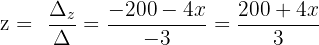
Considerando que las tres variables son números naturales, y que su suma es 100, obtenemos las siguientes soluciones:
| S1 | S2 | S3 | S4 | S5 | |
|---|---|---|---|---|---|
| x | 1 | 4 | 7 | 10 | 13 |
| y | 31 | 24 | 17 | 10 | 3 |
| z | 68 | 72 | 76 | 80 | 84 |
5 Se tienen tres lingotes compuestos del siguiente modo:
- El primero de 20 g de oro, 30 g de plata y 40 g de cobre.
- El segundo de 30 g de oro, 40 g de plata y 50 g de cobre.
- El tercero de 40 g de oro, 50 g de plata y 90 g de cobre.
Se pide qué peso habrá de tomarse de cada uno de los lingotes anteriores para formar un nuevo lingote de 34 g de oro, 46 g de plata y 67 g de cobre.
 = Peso del 1er lingote.
= Peso del 1er lingote.
 = Peso del 2º lingote.
= Peso del 2º lingote.
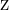 = Peso del 3er lingote.
= Peso del 3er lingote.
En el 1er lingote, la ley del oro es:

En el 2º lingote, la ley del oro es:

En el 3 er lingote, la ley del oro es:

La ecuación para el oro es:

En el 1er lingote, la ley de la plata es:

En el 2º lingote, la ley de la plata es:

En el 3 er lingote, la ley de la plata es:

La ecuación para el plata es:
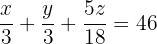
En el 1er lingote, la ley del cobre es:

En el 2ºlingote, la ley del cobre es:

En el 3 er lingote, la ley del cobre es:

La ecuación para el cobre es:
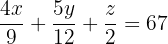
Reescribiendo las ecuaciones tenemos el siguiente sistema de ecuaciones:

Para resolver este sistema de 3x3 podemos ocupar el método de Kramer, es decir,

Aplicando este método a nuestro sistema de ecuaciones tenemos:



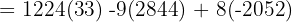
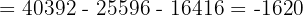

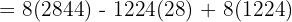


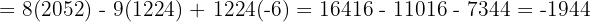
Finalmente, para encontrar los valores de cada incógnita:



Entonces la solución a nuestro sistema de ecuaciones es:
x = 45 y = 48 z = 54



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me ayudaria con este ejercicio
Tarea1
———
El Ministerio del Poder Popular para el Ecosocialismo proporciona tres tipos
de comida para tres tipos de especies de aves que alberga el aviario del Zoo
Aquarium de Valencia.
i) Cada ave de la especie 1 consume cada semana un promedio de 1 kilo
de alimento 1, 1 kilo de alimento 2 y 2 kilos de alimento 3.
ii) Cada ave de la especie 2 consume cada semana un promedio de 5 kilos
de alimento 1, 6 kilos de alimento 2 y 9 kilos de alimento 3.
iii) Cada ave de la especie 3 consume cada semana un promedio de 3 kilos
de alimento 1, 2 kilos de alimento 2 y 7 kilos de alimento 3.
Cada semana se proporciona al Zoo 350 kilos de alimento 1, 300 kilos de
alimento 2 y 750 kilos del alimento 3. Si se supone que las aves se comen todo
el alimento. ¿ Cuantas aves de cada especie pueden coexistir en el aviario?
Y asi quedaria la ecuacion:
+ 1 x1 + 5 y2 + 3 z3 = + 350
+ 1 x1 + 6 y2 + 2 z3 = + 300
+ 2 x1 + 9 y2 + 7 z3 = + 750
Me ayudarian en este caso..
Gracias
Tres resmas de papel tienen un valor de 33900
Cual es el precio de una resma
Me pueden ayudar con el procedimiento
Es un ejercicio planteamiento con resolución de ecuaciones lineales
Ayudenme por favor
33900/3 = 11300
El valor de una resma de papel es de 11300
Ecuaciones Lineales método Gauss Joroan
2×1-6×2-×3=-38
-3×1-×2+7×3=-34
-8×1-×2-2×3=-20
Multiplica por 4 la primera ecuacion y despues sumala con la que esta abajo se eliminara la y despues despeja la x que queda y encuentra su valor por ultimo usa una de las ecuaciones y sustituye el valor k encontraste en x y despeja la y listo
Para solucionar este problema debes plantear en primer lugar, la ecuación, la cual es la siguiente:
3*X = 33900
Luego de esto deberás despejar X, la cual corresponde al precio de una sola resma de papel, para ello deberás, pasar 33900 correspondiente a el precio total de las resmas de papel a dividir en 3, correspondiente al numero de resmas de papel, cabe mencionar que el precio total de las resmas de papel se divide en 3, puesto que 33900 estaba multiplicando, y por lo tanto al pasarlo al otro lado del igual automáticamente modifica su operación, en este caso el contrario de la multiplicación es la división, quedando así:
X=33900/3
Luego de hacer su respectiva operación, obtenemos como resultado final:
X=11300
Concluyendo finalmente que el valor de una sola resma de papel por el método de resolución de ecuaciones lineales corresponde a 11300