Capítulos
La programación lineal da respuesta a situaciones en las que se exige maximizar o minimizar funciones que se encuentran sujetas a determinadas limitaciones, que llamaremos restricciones.
Su empleo es frecuente en aplicaciones de la industria, la economía, la estrategia militar, etc.

Función objetivo
En esencia la programación lineal consiste en optimizar (maximizar o minimizar) una función objetivo, que es una función lineal de varias variables:

Restricciones
La función objetivo está sujeta a una serie de restricciones, expresadas por inecuaciones lineales:
 | 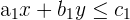 |
 | |
| ... ... ... | |
 |
Cada desigualdad del sistema de restricciones determina un semiplano.

Solución factible
El conjunto intersección, de todos los semiplanos formados por las restricciones, determina un recinto, acotado o no, que recibe el nombre de región de validez o zona de soluciones factibles.

Solución óptima
El conjunto de los vértices del recinto se denomina conjunto de soluciones factibles básicas y el vértice donde se presenta la solución óptima se llama solución máxima (o mínima según el caso).

Valor del programa lineal
El valor que toma la función objetivo en el vértice de solución óptima se llama valor del programa lineal.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
3. Un pequeño pero próspero negocio se dedica a la fabricación de Batas y Trusas en Medellín. Hacer una bata requiere 30 minutos de corte y 20 minutos de
fileteado. Hacer una trusa requiere 15 minutos de corte y 30 minutos de fileteado. La utilidad por cada bata fabricada y vendida es de 20.000 y la utilidad por
cada trusa fabricada y vendida es de 25.000. El negocio opera por un máximo de ocho (8) horas diarias. Su principal aliado es Batas de Seda S.A. una
comercializadora exitosa que le exige al menos la entrega de dos batas diarias. Determine cuantas batas y trusas deben ser fabricadas diariamente para
maximizar la utilidad de las ventas
una empresa desea maximizar sus ganancias mediante publicidad en television y redes sociales .Cada minuto de television genera 1000 unidades de ganancia y cada hora en redes sociales genera 500.El presupuesto es de 20,000 unidades y los costos son 200 por minuto de television y 1000 por hora en redes sociales .El maximo de horas en reds sociales es de 50 y en televisión es 30
Es un ejemplo de una ecuación utilizada en la programación lineal.
Pregunta 1Respuesta
a.
Y = 23 + 20×2 + 40y
b.
Z = x + 45y
c.
Z = x + 45y3
d.
Y = 20y + 20yx2
Un productor de alimento para animales, fabrica dos clases de grano, A y B. Cada unidad del grano A contiene 2 gramos de grasa, 1 gramo de proteína y 80 calorías. Cada unidad del grano B contiene 3 gramos de grasa, 3 gramos de proteína y 60 calorías. Suponga que el productor desea que cada unidad del producto final tenga, como mínimo, 18 gramos de grasa, 12 gramos de proteína y 480 calorías. Si cada unidad de A cuesta 10 centavos y cada unidad de B cuesta 12 centavos,
¿Cuántas unidades de cada clase de grano debe usar para minimizar el costo?
Alguien me ayuda con este problema: una empresa de transporte se comprometió a transportar 180.toneladas diarias de cemento desde un almacén central a una obra. La empresa tiene 8 camiones de tamaño mediano, cada uno puede transportar hasta 15 toneladas de cemento diariamente y 10 camiones grandes , cada uno puede transportar 20 toneladas de cemento diariamente. La empresa emplea 12 conductores y cada conductor puede conducir cada camión. El gasto diario promedio para un camión mediando es de 400 dolares y para un camión grande es de 600 dolares.
A) cuantos camiones de cada tipo debe manejar la empresa diariamente para que el gasto sea mínimo y aún así la empresa cumpla su compromiso?
B) si el gasto de un camión grande se reduce a 500 dolares. Cual será la respuesta de la pregunta (A).
Una carpintería fabrica dos diferentes modelos de mobiliario A y B. La venta los realiza en $300 y
$200, respectivamente. Para su realización necesita madera, aluminio y hierro. Se cuenta con 1800
m2, 4200m2 y 2100 m2 de cada material. Los consumos de madera, aluminio y hierro para cada tipo
de mobiliario están dados en la siguiente tabla
Madera 200 m3 Aluminio 200 m3 Hierro 300 m3
Madera 100 m3 Aluminio 300 m3 Hierro 100 m3
Una empresa tiene 100 horas de trabajo y $5,000 de presupuesto para producir dos
productos: A y B.
Producto A: 2 horas/unidad, $30/unidad, ganancia de $50/unidad.
Producto B: 3 horas/unidad, $40/unidad, ganancia de $60/unidad.
Objetivo: Maximizar las ganancias.
Restricciones:
2A + 3B ≤ 100 (horas)
30A + 40B ≤ 5000 (presupuesto)
Solver:
Objetivo: Maximizar ganancias = 50A + 60B
Variables: A, B
Restricciones: ≥ 0 y cumplir las ecuaciones anteriores.
me puedes ayudar con un ejercicio de programación lineal unos grandes almacenes desean liquidar 200 camisas y 10 pantalones de la temporada anterior. Para ello lanzan tres ofertas a, b y c la oferta A consiste en consiste en un lote de una camisa y un pantalón , que se venden a 30$ la oferta B consiste en un lote de tres camisas y un pantalón que se venden a 50$ y la oferta C consiste en un lote de 2 camisas y 2 pantalones que se venden en 40 $. no se desea ofrecer menos de 20 lotes de la oferta A ni menos de 10 de la B, ni menos de 15 lotes de la oferta C. ¿cuantos lotes ha de vender de cada tipo para maximizar la ganancia? formule el modelo de programacion lineal.
Este es un problema de optimización lineal. Se puede formular como sigue:
**Variables de decisión:**
* x1: Número de porciones de galleta
* x2: Número de porciones de sorbete
* x3: Número de porciones de refresco
* x4: Número de porciones de pastel de queso
**Función objetivo:**
Minimizar el coste: \[0.5×1 + 0.2×2 + 0.3×3 + 0.8×4\]
**Restricciones:**
* Calorías: \[400×1 + 200×2 + 150×3 + 500×4 ≥ 500\]
* Chocolate: \[3×1 + 2×2 + 0x3 + 0x4 ≥ 6\]
* Azúcar: \[2×1 + 2×2 + 4×3 + 4×4 ≥ 10\]
* Grasa: \[2×1 + 4×2 + 1×3 + 5×4 ≥ 8\]
* No negatividad: \[x1, x2, x3, x4 ≥ 0\]
Para resolver este problema se puede usar el método simplex o cualquier software de optimización lineal. La solución proporcionará los valores óptimos de x1, x2, x3 y x4 que minimizan el coste al tiempo que cumplen todas las restricciones.
Ayuda con este problema