Los/las mejores profesores/as de Matemáticas que están disponibles
José arturo
16€
/h
¡1a clase gratis!
Francisco javier
12€
/h
¡1a clase gratis!
Fátima
18€
/h
¡1a clase gratis!
Lautaro
14€
/h
¡1a clase gratis!
Alex
13€
/h
¡1a clase gratis!
José angel
6€
/h
¡1a clase gratis!
Santiago
15€
/h
¡1a clase gratis!
Pedro
12€
/h
¡1a clase gratis!
José arturo
16€
/h
¡1a clase gratis!
Francisco javier
12€
/h
¡1a clase gratis!
Fátima
18€
/h
¡1a clase gratis!
Lautaro
14€
/h
¡1a clase gratis!
Alex
13€
/h
¡1a clase gratis!
José angel
6€
/h
¡1a clase gratis!
Santiago
15€
/h
¡1a clase gratis!
Pedro
12€
/h
¡1a clase gratis!
Propiedades de la matriz inversa
1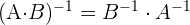 
2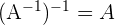 
3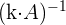 
4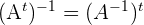 
Cálculo por el método de Gauss
Sea 
una matriz cuadrada de orden 
. Para calcular la matriz inversa de , que denotaremos como 
, seguiremos los siguientes pasos:
1 Construir una matriz del tipo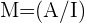 
, es decir, está en la mitad izquierda de 
y la matriz identidad 
en la derecha.
Consideremos una matriz 
arbitraria:
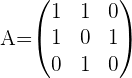
La ampliamos con la matriz identidad de orden 3.
2 Utilizando el método Gauss vamos a transformar la mitad izquierda, , en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: .
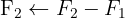
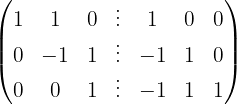
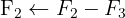
La matriz inversa es:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Funcion inversa de
b=f(x)=x-7/3
Hola, en ecuaciones matriciales, en el ejercicio 4, los valores de B y de C están intercambiados en la solución
Ya lo revise y no veo lo que mencionas. La matriz C solo se usa para la multiplicación con la suma de la inversa de A y B.
Buenas, parece haber un error en el ejercicio 3 , de AX=B: A=[1 3][1 4] y B=[1 -1][3 1], porque la respuesta que ustedes dan es: X=[1 -5][0 4], y a mi me da: X=[-5 -7][2 2], no se si es error mío o suyo, ya que lo confirmé con calculadora externa y mi respuesta está bien.
𝐴 =
[2 −1
3 1]
Una disculpa ya se corrigió.
8(3 * 7) matrix ]-\ (3*(4*-12)\ +16*(2-978
Cuales son los pasos para resolver una ecuacion x matrices y escribe sus fórmulas
2x-z=14
4x+y-z=41
3x-y+5x=53