Temas
Definición de determinante
A cada matriz cuadrada 
se le asigna un escalar particular denominado determinante de , denotado por 
o por 
Este escalar permite caracterizar algunas propiedades de la matriz, por ejemplo, el determinante de es no nulo sí y sólo sí es invertible.
A continuación veremos cuál es el valor del determinante de matrices de orden menor o igual a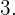 
Determinante de orden uno
Dada la matriz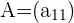 
,
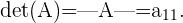
Determinante de orden dos
Dada la matriz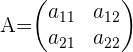 
,
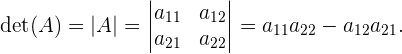
Determinante de orden tres
Dada la matriz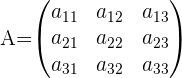 
,
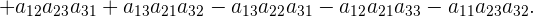
Regla de Sarrus
La regla de Sarrus es una algoritmo sencillo de memorizar y sirve para calcular el determinante de una matriz de orden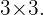 
El método consiste en lo siguiente, debemos hallar factores positivos y factores negativos, a través de los siguiente pasos.
Los términos con signo positivo están formados por los elementos de la diagonal principal y los de las diagonales paralelas con su correspondiente vértice opuesto.
La siguiente figura nos indica cuáles posiciones de la matriz debemos multiplicar.
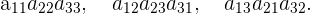
Los términos con signo negativo están formados por los elementos de la diagonal secundaria y los de las diagonales paralelas con su correspondiente vértice opuesto.
La siguiente figura nos indica cuáles posiciones de la matriz debemos multiplicar.
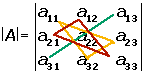
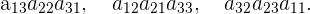
Menor complementario
Se llama menor complementario de un elemento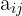 
al valor del determinante de orden 
que se obtiene al suprimir en la matriz la fila 
y la columna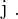 
Adjunto
Se llama adjunto del elemento 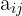al menor complementario anteponiendo:
- El signo es
si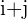 
es par. - El signo es
si 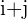es impar.
El valor de un determinante es igual a la suma de productos de los elementos de una línea por sus adjuntos correspondientes:
Determinante de orden superior a tres
Describiremos con algunos pasos cómo calcular el determinante de una matriz de orden superior a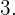
1 Si alguna de las filas o columnas de la matriz tiene todos sus elementos nulos, entonces el determinante será igual a cero.
2 En caso de que no hayan filas o columnas nulas, entonces elegimos la fila número uno.
3 Dado un elemento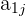 
de la fila uno, debemos calcular el determinante de la matriz que resulta de eliminar la fila 
y columna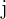 
de la matriz 
4 Multiplicamos el valor del determinante calculado en el paso 3 con el número 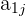y esto lo hacemos para cada elemento 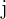de la matriz
5 Finalmente debemos sumar y restar de manera alternativa los valores calculados en los pasos anteriores. Es decir, el valor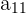 
por el determinante de la matriz resultante de eliminar la fila y la columna lleva signo positivo; la siguiente valor lleva signo negativo, el siguiente signo negativo y así sucesivamente. El resultado final es el determinante de la matriz
Propiedades de los determinantes
Dada una matriz 
sea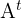 
su transpuesta.
1 
2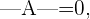 
si alguna de las siguientes afirmaciones se cumple: la matriz posee dos filas iguales, todos los elementos de alguna fila son iguales a ceros o los elementos de una fila son combinación lineal de otras líneas.
3 Un determinante triangular es igual al producto de los elementos de la diagonal principal, donde una matriz triangular es aquella que tiene todos sus elementos por encima o debajo de la diagonal principal igual a cero.
4 Si en un determinante se cambian entre sí dos líneas paralelas su determinante cambia de signo.
5 Si a los elementos de una línea se le suman los elementos de otra paralela multiplicados previamente por un número real el valor del determinante no varía.
6 Si se multiplica un determinante por un número real, queda multiplicado por dicho número cualquier línea, pero sólo una.
7 Si todos los elementos de una fila o columna están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes.
8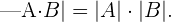 
Matriz inversa
Dada una matriz , su inversa esta dada por
donde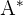 
es la matriz adjunta de
Rango de una matriz
El rango es el orden de la mayor submatriz cuadrada no nula.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola. Una sugerencia:
En el aparte 5, sugiero añadir algo a la explicación de la regla de invariancia citada previamente.
La original dice: “Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.”
La sugerencia sería: “Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás y de ella misma, el valor del determinante no varía.”
Espero que eso ayude…
Gracias por estar ahí… Saludos!!
Fijate que me aparece el articulo “Ejercicios de determinantes II” y no encuentro lo que mencionas, podrias indicarme el articulo que mencionas, gracias por la sugerencia.
Colo resolver el método de determinante de
5×-2y=1
3×+y=5
(1-1 0 0 2 1 1 3 -1