¡Bienvenido a los desafiantes ejercicios de determinantes! En esta serie de prácticas, nos sumergiremos en el emocionante mundo de las matrices y los determinantes, una poderosa herramienta matemática con aplicaciones en diversas áreas, como la física, la ingeniería, la economía y más.
Los determinantes son valores numéricos que se calculan a partir de una matriz y nos proporcionan información crucial sobre sus propiedades lineales y su comportamiento en sistemas de ecuaciones lineales. A lo largo de estos ejercicios, aprenderemos a calcular determinantes para matrices de diferentes tamaños y a interpretar sus resultados. ¡Comencemos a descubrir los secretos de los determinantes juntos!
1Si el valor del determinante

Calcular el valor de:

Cada una de las filas de  esta multiplicada por
esta multiplicada por  entonces por propiedades de determinantes tenemos que
entonces por propiedades de determinantes tenemos que

Ahora aplicaremos las siguiente operaciones columna y fila a la matriz 
Primero cambiamos las columnas  y
y 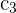 y luego cambiamos las filas
y luego cambiamos las filas  y
y 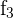 , esto es,
, esto es,

Recordemos que mover filas o columnas de la matriz solo altera el valor del determinante en el signo. Como hicimos dos movimientos entonces seria menos por menos lo que nos da mas, entonces

2Demostrar que el siguiente determinante es divisible por  :
:

Para demostrar lo pedido, lo que haremos será sumar a la columna  cada una de las otras columnas, es decir, empezamos sumando la columna
cada una de las otras columnas, es decir, empezamos sumando la columna  y la columna
y la columna  , luego este resultado le sumamos la columna
, luego este resultado le sumamos la columna  y asi sucesivamente hasta llegar a la columna
y asi sucesivamente hasta llegar a la columna  . Recordemos que hacer este tipo de operaciones elementales no afecta el valor del determinante.
. Recordemos que hacer este tipo de operaciones elementales no afecta el valor del determinante.

Ahora podemos sacar el factor  de la columna
de la columna  . Lo que nos da
. Lo que nos da


De esta forma tenemos que el determinante inicial es divisible por  .
.
3Aplicando las propiedades de los determinantes, calcular:

Primero recordemos que restar o sumar filas o columnas no afecta el resultado del determinante. Ahora haremos los cálculos de manera estructura indicando con los siguiente símbolos las operaciones que vayamos realizando.  significa que a la fila
significa que a la fila  le sumamos o le restamos la fila
le sumamos o le restamos la fila 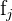 , similarmente
, similarmente 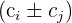 significa que a columna
significa que a columna 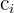 le sumamos o le restamos la columna
le sumamos o le restamos la columna  . Empezamos con la matrix
. Empezamos con la matrix  ,
,


El determinante es cero porque al final obtenemos dos columnas linealmente dependientes.
Continuamos con la matriz  ,
,



Finalmente para  tenemos que
tenemos que


4Calcular el valor de los siguientes determinantes:

Primero recordemos que restar o sumar filas o columnas no afecta el resultado del determinante. Ahora haremos los cálculos de manera estructura indicando con los siguiente símbolos las operaciones que vayamos realizando.  significa que a la fila
significa que a la fila  le sumamos o le restamos la fila
le sumamos o le restamos la fila 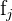 , similarmente
, similarmente 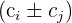 significa que a columna
significa que a columna 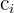 le sumamos o le restamos la columna
le sumamos o le restamos la columna  . Empezamos con la matrix
. Empezamos con la matrix  ,
,





Continuamos con la matriz  ,
,


5¿Para qué valores de  la matriz
la matriz

no admite matriz inversa?
Primero calculemos el determinante de la matriz,

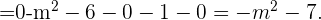
Para que la matriz no admita una inversa se debe cumplir que

Dado que 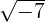 no pertenece a los números reales podemos concluir que la matriz siempre admite una inversa.
no pertenece a los números reales podemos concluir que la matriz siempre admite una inversa.
6¿Para qué valores de  la matriz
la matriz

no admite matriz inversa?
Primero calculemos una matriz equivalente de  ,
,

Ahora calculamos el determinante de la matriz equivalente,

Para que la matriz no admita una inversa se debe cumplir que
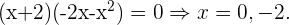
Podemos concluir que la matriz no admite inversa para 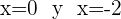 .
.
7Encuentra el valor de  para la ecuación
para la ecuación

Primero calculemos una matriz equivalente,

Ahora calculamos el determinante de la matriz equivalente e igualamos a cero,

Resolviendo la última igualdad, se tiene que
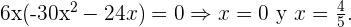
8Si

Encuentra el valor de

Primero observamos que la primera columna tiene como factor común  , entonces
, entonces

Observamos que la segunda columna tiene como factor común  , entonces
, entonces

Encontramos una matriz equivalente

conocemos el valor del último determinante, por lo que sustituimos y obtenemos

9Resolver la ecuación matricial:

donde  .
.
Dado que  , podemos decir que existe
, podemos decir que existe  . Al multiplicar a la derecha en ambos lados de la igualdad tenemos que
. Al multiplicar a la derecha en ambos lados de la igualdad tenemos que

10Resolver las ecuación matricial:

donde  .
.
Dado que  , podemos decir que existe
, podemos decir que existe  . Al multiplicar en ambos lados de la igualdad tenemos que
. Al multiplicar en ambos lados de la igualdad tenemos que



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola. Una sugerencia:
En el aparte 5, sugiero añadir algo a la explicación de la regla de invariancia citada previamente.
La original dice: “Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.”
La sugerencia sería: “Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás y de ella misma, el valor del determinante no varía.”
Espero que eso ayude…
Gracias por estar ahí… Saludos!!
Fijate que me aparece el articulo “Ejercicios de determinantes II” y no encuentro lo que mencionas, podrias indicarme el articulo que mencionas, gracias por la sugerencia.
Colo resolver el método de determinante de
5×-2y=1
3×+y=5
(1-1 0 0 2 1 1 3 -1