Temas

Propiedades de los determinantes
1Demostrar, sin desarrollar, que los siguientes determinantes valen cero:

1 Determinante de A
A la columna 3 le sumamos la columna 2 y obtenemos:

Tiene dos columnas iguales, por lo tanto su determinante debe ser igual a 0.
2 Determinante de B
Notamos que la tercera columna es igual a la suma de las otras dos, así que su determinante es 0.

 , calcula los determinantes
, calcula los determinantes  y
y 
1 Determinante de B

2 Determinante de C


1 Determinante de A

No nos interesa saber el valor exacto de la última matriz, pues sabemos que debe ser un número entero y que al multiplicarse por el 5 de la izquierda, el determinante de  resultará un múltiplo de 5.
resultará un múltiplo de 5.
2 Determinante de B

De manera análoga, ignoramos el valor exacto de la última matriz, ya que al ser un número entero y al multiplicarse por el 4 de la izquierda, el determinante de  resultará un múltiplo de 4
resultará un múltiplo de 4


No nos interesa saber el valor exacto de la última matriz, pues sabemos que debe ser un número entero y que al multiplicarse por el 15 de la izquierda, el determinante de resultará un múltiplo de 15
1 
Expresamos la matriz como suma de dos matrices

Cada uno de estos sumandos es a su vez la suma de otras dos matrices

Pero la segunda y tercera matriz tiene dos columnas iguales, por lo que su determinante será cero. Así que

Separamos como sumas nuevamente estas dos matrices y nos queda

Nuevamente la segunda y tercera matriz tiene dos columnas iguales, por lo que su determinante será cero.


Cada factor  sale de haber intercambiado la posición de un par de columnas
sale de haber intercambiado la posición de un par de columnas
2 
Multiplicamos la 1ª fila por la  , la 2ª por
, la 2ª por  y la tercera por
y la tercera por  , por tanto tenemos que dividir por abc para que el resultado no varíe.
, por tanto tenemos que dividir por abc para que el resultado no varíe.


1 Determinante A

2 Determinante B

3 Determinante C

Ecuaciones y determinantes
7Resolver las siguientes ecuaciones sin desarrollar los determinantes.
1 

Calculamos el determinante y resulta la ecuación
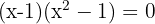
Las soluciones son entonces

2 

De calcular el determinante resulta

Las soluciones son

-
-
 , donde
, donde
-

-
-
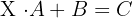 donde
donde
-

1 
 , existe la matriz inversa
, existe la matriz inversa 
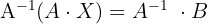
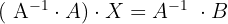
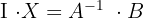
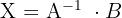


2 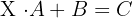
 , existe la matriz inversa
, existe la matriz inversa 

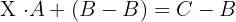



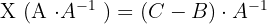
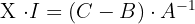




Determinantes triangulares
9Pasando a determinantes triangulares, calcular el valor de:

1 Determinante A



2 Determinante B

Determinantes de Vandermonde
10Calcular los determinantes de Vandermonde:

1 Determinante A



2 Determinante B






Matriz inversa
11Hallar la matriz inversa de:


La matriz adjunta y la matriz adjunta transpuesta están dadas por

Finalmente la inversa es

12Para qué valores de  la matriz
la matriz  no admite matriz inversa?
no admite matriz inversa?
Calculamos el determinante

Para  la matriz
la matriz  no tiene inversa.
no tiene inversa.
Rango de matrices
13Calcular el rango de las siguientes matrices:
1 Rango de A





Por lo tanto el rango es
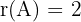
2 Rango de B





Entonces el rango de  está dado por
está dado por

3 Rango de C

Eliminamos la tercera columna por ser nula, la cuarta por ser proporcional a la primera, y la quinta porque combinación lineal de la primera y segunda:
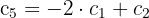
El rango de  es equivalente al rango de la siguiente matriz
es equivalente al rango de la siguiente matriz


El rango de  es
es
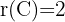















Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hola. Una sugerencia:
En el aparte 5, sugiero añadir algo a la explicación de la regla de invariancia citada previamente.
La original dice: “Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.”
La sugerencia sería: “Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás y de ella misma, el valor del determinante no varía.”
Espero que eso ayude…
Gracias por estar ahí… Saludos!!
Fijate que me aparece el articulo “Ejercicios de determinantes II” y no encuentro lo que mencionas, podrias indicarme el articulo que mencionas, gracias por la sugerencia.
Colo resolver el método de determinante de
5×-2y=1
3×+y=5
(1-1 0 0 2 1 1 3 -1