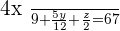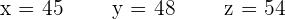Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12

Exercise 1
John purchased a computer and a TV for  dollars and later sold both items for
dollars and later sold both items for 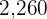 dollars.
dollars.
How much did each item cost, knowing that John sold the computer for  % more than the purchase price, and the TV for
% more than the purchase price, and the TV for  % more?
% more?
Exercise 2
What is the area of a rectangle knowing that its perimeter is  cm and its base is three times its height?
cm and its base is three times its height?
Exercise 3
A farm has pigs and turkeys, in total there are  heads and
heads and 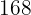 paws. How many pigs and turkeys are there?
paws. How many pigs and turkeys are there?
Exercise 4
John says to Peter, "I have double the amount of money that you have" and Peter replies, "if you give me six dollars we will have the same amount of money". How much money does each have?
Exercise 5
A company employs  people. Of this amount,
people. Of this amount,  % of the men wear glasses and
% of the men wear glasses and  % of the women also wear glasses. If the total number of people who wear glasses is
% of the women also wear glasses. If the total number of people who wear glasses is  , how many men and women are there in the company?
, how many men and women are there in the company?
Exercise 6
The value of the digit in the tens column of a two-digit number is twice the value of the digit in the one's column, and if you subtract this by number  , the number obtained is a number with the same digits but in reverse order. What is the number?
, the number obtained is a number with the same digits but in reverse order. What is the number?
Exercise 7
Two appliances have been purchased for 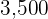 dollars. If a
dollars. If a  % discount was applied to the first item and an
% discount was applied to the first item and an  % discount on the second, the total price for both purchases would have been
% discount on the second, the total price for both purchases would have been  dollars. What is the price of each item?
dollars. What is the price of each item?
Exercise 8
Find a two-digit number knowing that its digit in the tens column minus  is the same digit in the one's column and if the order of the digits is reversed, the number obtained is equal to the first number, minus
is the same digit in the one's column and if the order of the digits is reversed, the number obtained is equal to the first number, minus  .
.
Exercise 9
A company has three mines with ore deposits:
| Nickel (%) | Copper (%) | Iron (%) | |
|---|---|---|---|
| Mine A |  |  |  |
| Mine B |  |  |  |
| Mine C |  |  |  |
How many tons from each mine should be used to obtain  tons of nickel,
tons of nickel,  tonnes of copper, and
tonnes of copper, and  tons iron?
tons iron?
Exercise 10
The age of a father is twice the sum of the ages of his two sons. Some years ago (exactly the difference of the current ages of children), the father's age was three times the sum of the ages of his sons. After some years (the amount that is equal to the sum of the current age of the children), the sum of the ages of all three will be  years. How old was the father when his sons were born?
years. How old was the father when his sons were born?
Exercise 11
Three types of grain are sold by a farmer: wheat, barley, and millet.
Each portion of wheat sells for  dollars, the barley for
dollars, the barley for  dollars, and the millet for
dollars, and the millet for 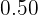 dollars.
dollars.
If he sells  portions in total and receives
portions in total and receives  dollars from the sale, how many portions are sold of each type?
dollars from the sale, how many portions are sold of each type?
Exercise 12
There are three ingots.
- The first of
 grams of gold,
grams of gold,  grams of silver, and
grams of silver, and  grams of copper.
grams of copper. - The second of
 grams of gold,
grams of gold,  grams of silver, and
grams of silver, and  grams of copper.
grams of copper. - The third of
 grams of gold,
grams of gold,  grams of silver, and
grams of silver, and  grams of copper.
grams of copper.
What weight will be taken from each of the previous ingots to form a new ingot of  grams of gold,
grams of gold,  grams of silver, and
grams of silver, and  grams of copper?
grams of copper?
Solution of exercise 1
John purchased a computer and a TV for  dollars and later sold both items for
dollars and later sold both items for 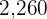 dollars.
dollars.
How much did each item cost, knowing that John sold the computer for  % more than the purchase price, and the TV for
% more than the purchase price, and the TV for  % more?
% more?
x price of the computer.
y price of the TV.
 price of sale of the computer.
price of sale of the computer.
 price of sale of the TV.
price of sale of the TV.
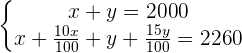

If we add both equations, we will be left with 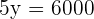
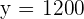
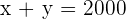
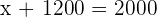
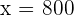
800 dollar price of the computer.
1,200 dollar price of the TV.
Solution of exercise 2
What is the area of a rectangle knowing that its perimeter is  cm and its base is three times its height?
cm and its base is three times its height?
x base of the rectangle.
y height of the rectangle.
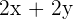 perimeter.
perimeter.
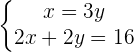
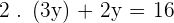
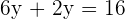


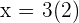

6 cm base of the rectangle.
2 cm height of the rectangle.
Solution of exercise 3
A farm has pigs and turkeys, in total there are  heads and
heads and 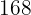 paws. How many pigs and turkeys are there?
paws. How many pigs and turkeys are there?
x number of turkeys.
y number of pigs.
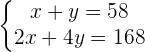
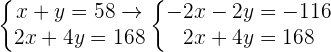



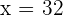
32 number of turkeys.
26 number of pigs.
Solution of exercise 4
John says to Peter, "I have double the amount of money that you have" and Peter replies, "if you give me six dollars we will have the same amount of money". How much money does each have?
x John's money.
y Peter's money.
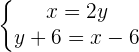
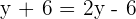
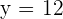
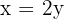
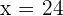
24 John's money.
12 Peter's money.
Solution of exercise 5
A company employs  people. Of this amount,
people. Of this amount,  % of the men wear glasses and
% of the men wear glasses and  % of the women also wear glasses. If the total number of people who wear glasses is
% of the women also wear glasses. If the total number of people who wear glasses is  , how many men and women are there in the company?
, how many men and women are there in the company?
x number of men.
y number of women.
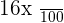 men with glasses.
men with glasses.
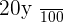 women with glasses.
women with glasses.

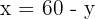


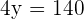

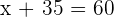

25 number of men.
35 number of women.
Solution of exercise 6
The value of the digit in the tens column of a two-digit number is twice the value of the digit in the one's column, and if you subtract this by number  , the number obtained is a number with the same digits but in reverse order. What is the number?
, the number obtained is a number with the same digits but in reverse order. What is the number?
x units (ones column)
y tens (tens column)
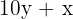 number
number
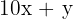 number reversed
number reversed

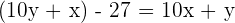
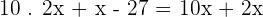



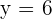
The number is 63
Solution of exercise 7
Two appliances have been purchased for 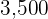 dollars. If a
dollars. If a  % discount was applied to the first item and an
% discount was applied to the first item and an  % discount on the second, the total price for both purchases would have been
% discount on the second, the total price for both purchases would have been  dollars. What is the price of each item?
dollars. What is the price of each item?
x price of the 1st.
y price of the 2nd.
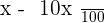 discount on the 1st.
discount on the 1st.
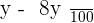 discount on the 2nd.
discount on the 2nd.

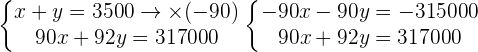


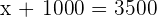
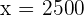
2,500 dollars price of the 1st.
1,000 dollars price of the 2nd.
Solution of exercise 8
Find a two-digit number knowing that its digit in the tens column minus  is the same digit in the one's column and if the order of the digits is reversed, the number obtained is equal to the first number, minus
is the same digit in the one's column and if the order of the digits is reversed, the number obtained is equal to the first number, minus  .
.
x unit
y ten
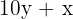 number
number
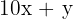 number reversed
number reversed

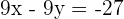


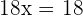

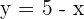

Number 41
Solution of exercise 9
A company has three mines with ore deposits:
| Nickel (%) | Copper (%) | Iron (%) | |
|---|---|---|---|
| Mine A |  |  |  |
| Mine B |  |  |  |
| Mine C |  |  |  |
How many tons from each mine should be used to obtain  tons of nickel,
tons of nickel,  tonnes of copper, and
tonnes of copper, and  tons iron?
tons iron?
x = tons of mine A. x=200 t
y = tons of mine B. y=100 t
z = tons of mine C. z=300 t

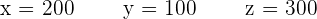
Solution of exercise 10
The age of a father is twice the sum of the ages of his two sons. Some years ago (exactly the difference of the current ages of children), the father's age was three times the sum of the ages of his sons. After some years (the amount that is equal to the sum of the current age of the children), the sum of the ages of all three will be  years. How old was the father when his sons were born?
years. How old was the father when his sons were born?
x = Current age of the father.
y = Current age of the eldest son.
z = Current Age of youngest son.
Current Relationship: 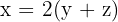
It y - z years 
Within y + z: 
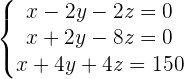

At birth, children, the father was 35 and 40, respectively.
Solution of exercise 11
Three types of grain are sold by a farmer: wheat, barley, and millet.
Each portion of wheat sells for  dollars, the barley for
dollars, the barley for  dollars, and the millet for
dollars, and the millet for 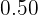 dollars.
dollars.
If he sells  portions in total and receives
portions in total and receives  dollars from the sale, how many portions are sold of each type?
dollars from the sale, how many portions are sold of each type?
x = volume of wheat.
y = Volume of barley.
z = Volume of millet.


Considering that the three variables are natural numbers, and that their sum is 100, the following solutions are obtained:
<tableclass="t_izq" style="margin-left:5%;">
S1 S2 S3 S4 S5 x1471013y312417103z6872768084
Solution of exercise 12
There are three ingots.
- The first of
 grams of gold,
grams of gold,  grams of silver, and
grams of silver, and  grams of copper.
grams of copper. - The second of
 grams of gold,
grams of gold,  grams of silver, and
grams of silver, and  grams of copper.
grams of copper. - The third of
 grams of gold,
grams of gold,  grams of silver, and
grams of silver, and  grams of copper.
grams of copper.
What weight will be taken from each of the previous ingots to form a new ingot of  grams of gold,
grams of gold,  grams of silver, and
grams of silver, and  grams of copper?
grams of copper?
x = weight of the 1st ingot.
y = weight of the 2nd ingot.
z = weight of the 3rd ingot.
Gold
In the 1st ingot, the law is: 
In the 2nd ingot, the law is: 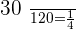
In the 3rd ingot, the law is: 
The equation for gold is:

Silver
In the 1st ingot, the law is: 
In the 2nd ingot, the law is: 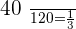
In the 3rd ingot, the law is: 
The equation for the silver is:
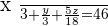
Copper
In the 1st ingot, the law is: 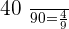
In the 2nd ingot, the law is: 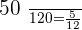
In the 3rd ingot, the law is: 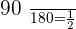
The equation for copper is: